
Warning! randint()
in Attaway has been replaced by
randi(). Use
>> help (randi, randint, rand) and be careful!
Programming Assignment 1
(Code and Readme: 100%, Writeup 0%)
Assigned Tuesday, Jan 18, 2011; Due Tuesday, Jan 25, 2011.
Attaway Chapter 1 Exercises:
For Edition 1:
Do all of these from 7 to 38 inclusive
EXCEPT numbers 18, 19, 20, 28, 32.
Extra Problem: What does M([1 2],:) = M([2 1],:); do?
Give an answer using the book and your head, and then verify your
answer with Matlab.
For Edition 2:
Do all of these from 7 to 42 inclusive
EXCEPT numbers 8,10, 20, 21, 22, 33, 39. 40.
Extra Problem: What does M([1 2],:) = M([2 1],:); do?
Give an answer using the book and your head, and then verify your
answer with Matlab.
Some hints and observations on some of the problems are given below.
Make sure you know what directory Matlab is using. Use >> pwd
to find out. We highly recommend on UR Laboratory machines
that you be in
C:\testing\Documents\MATLAB\
since very mysterious errors can happen if you're not. If you've got
a
zip drive, put its contents into the above directory and reload it
from that directory when you're finished. Matlab will save your files
and changes into this directory if you start there.
If you're NOT in this directory, go there with
>> cd C:/testing/Documents/MATLAB/
Using backslashes like
>> cd C:\testing\Documents\MATLAB
might work too.
Make a single script called main.m with comment lines giving the assignment (here, "Programming 1") and your name on the top.
The first and last executable lines of main.m are: diary and diary off, respectively. That will make a record of your output in the file diary.
The script main.m contains all the little code snippets the questions call for. Use comments to number the snippets. Use comments for the requested short answers or observations.
My session might look like this if I started with exercise 8 (Ed. 1) = 9 (Ed. 2) I'm showing some matlab output interleaved with my main.m script.
% main.m for %Programming Exercise 1. %Chris Brown diary % turn on the diary % 8 (or 9). >>ftemp = 98.6; myage = 98.6000 %matlab will print this, it'll go in diary >> ctemp = %my formula ... % 9 (11) >> help elfun ... diary off %%% end of main.m
Don't go right to the exercises and start flipping back thru the chapter hoping to find the relevant bit. That sort of brainless thoughtless pattern-matching (thought = google) doesn't generalize, so lose that habit PDQ. Your goal is NOT to do the exercises, the goal is to learn the material. Exercises are part of the means, not the end. Read and try out things from the whole chapter first.
Ed. 1 26 (Ed. 2 28): Attaway 1.5.1.1, use range expression (with : or :s) (sometimes she calls it an iterator). This one needs a step value not = 1. Attaway 1.5.4 end is useful.
Ed 1 27 (Ed. 2 29): That is, as close to halves as you can get. If they're not equal, then 1st is 1 longer than second or vice-versa. Again, easy with end, fix() and ranges.
Ed. 1 35 (Ed. 2 36):
rand(x,y) returns a matrix of the given size
full of random numbers between 0 and 1 (>>help rand).
If every one of them is scaled and shifted (multiplied by and added to a
constant), you can stretch and shift their values to be between -5 and
5, right? This question seems a little unfair because I don't think
Attaway has told you that one can multiply a matrix by a number, as in
Mat2 = 7*Mat1;
That works fine, is called scalar-matrix multiplication, and multiplies each
matrix element by the scalar.
We can't add or subtract scalars elementwise to a matrix in this
fashion, so we have to
create a matrix (probably with ones of the same size, multiply it
by the number we want to add or subtract from our original matrix's elements,
and then subtract that, as in
Mat2 = Mat1 - 7*ones(3,5);
Ed. 1 37 (Ed. 2 38): This is a one-liner: Attaway 1.5.6.
Programming Assignment 2
(Code and Readme: 100%, Writeup 0%)
See the Working Directory section in Assignment 1.
Also see the Universal Hand-In Information.
For this assignment we'll need seven .m files for functions. and a main script file named main.m, which calls and demonstrates the functions. You'll produce a "diary" file using the diary and diary off commands, which is to be handed in as well.
Your name should be at the top of the main script. If we type main we should get a run of all the exercises. The a diary file made as in Assignment I. Last, you'll need a README file that explains what each .m file does.
Attaway:
(Ed. 1):Chapter 5: Questions 1, 2, 3, 5, 7, 8.
(Ed. 2):Chapter 6: Questions 1, 2, 3, 5, 6, 7.
Also the two functions below:
1. Vector Addition Once:
Write a function vec_add()
that takes two (row or column) vectors and returns their sum.
Also 2. Vector Addition Twice: In your main.mscript,
write one matlab assignment statement that uses vec_add()
to add three vectors and return their sum.
You'll thus write eight .m files and a script main.m
that calls each of your eight functions with some arguments to
convince the reader they're working:
For instance, the latter part of your script might look like:
... % Vector Addition Once v1 = vec_add([1 2 3], [4 5 6]) newvec = vec_add([1 2 3]', [4 5 6]') v3 = vec_add([1 2 3]', [4 5 ]') % should cause error % Vector Addition Twice v_clever = ...
How to proceed: CB would do this: write a main.m template that looks like
% ex 1 % ex 2 ... % vector add once % vector add twice
and save it as main.m Then go write a function for exercise 1 in a .m file. Debug it: make sure it works. You can work in the command window, but I would use the main.m script for the test cases. You should leave off ; in your test function calls so that they return a visible result. Run the tests until they work, editing your function to fix errors. Note what you've done: the same tests that convince you your function works should convince the grader, so you are done with exercise 1.
Repeat for all exercises, adding tests to main.m as you debug the function. The end result is a main.m script that consists of several tests of each of the functions you've written. (And a single statement for "Vector Addition Twice"). When you execute main.m by typing main at the command window prompt, you should get several screenfuls of output showing that all your functions work. At that point you're ALMOST done.
Last, type
>>diary >>main ... lots of answers scroll by in the command window... >>diary off
in the command window and you now have a transcript file in your directory called diary that captures the output. OR you can edit the diary commands into the start and end of main.m, run it, and get the same result.
Now you zip archive and submit all your .m files,
the main.m script, and the
diary file as per instructions on the main page.
Programming Assignment 3
(Code and Readme: 100%, Writeup 0%)
See the Working Directory section in Assignment 1. Also see the Universal Hand-In Information.
For this assignment we'll need a passel of .m files for functions and scripts, and a main script file named main.m, which calls and demonstrates your scripts and functions. Your name should be at the top of the main script. If we type main we should get a run of all the exercises. Create a diary using one of the methods mentioned in Assignment 2. And also a README file that explains what each .m file does.
We'd expect Chapter 3 exercises to deal with aspects of selection statements, but from now on we're allowed and expected to use everything we've learned in all assignments. The "Extras for Labs" problems are for use in labs for practice, and may be handed in along with the assigned Chap. 3 questions for extra credit. If everything is done in exemplary style they can raise a 3 to a 4, but doing more problems in a mediocre way is still mediocre work, so lots of problems at the 2-mark level don't add up to a 3. Work eight (8) of the Extras for a possible extra mark.
Attaway: Edition 1:
Chapter 3: Questions 1*, 9*(function, not script), 11*
(function, not script), 12* (function) , 18*, 22, 30.
(* means 'see notes below').
Extra Questions for Labs and Extra Credit: 2.22, 2.27, 2.28, 2.29,
2.31; 3.3, 3.10, 3,14 (write a function, not script!), 3.15, 3.20
(function, not script!).
Edition 2:
Chapter 3: Questions 1*, 9*(function, not script), 13*
(function, not script), 14* (function), 20*, 27, 30.
(* means 'see notes below').
Extra Questions for Labs and Extra Credit: 2.22, 2.26, 2.27,
2.30, 2.32; 3.3, 3.11, 3,16 (write a function, not script!).
Notes: Ch3. Q.1: Also answer for the expression my_mat > 5
if my_mat = [3 4 5 6 7 6 5 4 3]. What's going on here?
(hint: vectorization)
Q.9: your function takes the two values as input.
Q.11 (= Ed.2 13): your function has no arguments, performs as described.
Q.12 (Ed2. 14) seems to depend on prior Question,
but of course we mean 'write a function
solving the problem of [Q.11, Q.13) using a switch instead.'
Q. 18. (Ed2. 20)
Pythagorean triples are tons of fun!
Don't forget the comments.
Programming Assignment 4
(Code and Readme: 100%, Writeup 0%)
See the Working Directory section in Assignment 1. Arrangements same as Prog. Asst. 3 above. Work all the Extras for a possible extra mark.
There are six more problems below (root-finding, accumulation, two matrices, two statistics). First, here are notes on those above.
Q.19 (Ed 2 21) USE LOOPS (in fact two nested for loops)! Here issue is that the ranges, like -20:5:55, are not useful indexes for your array. Your function (maybe called WCF) could take the ranges in as arguments, or could have no arguments and use the given ranges. In any event, I recommend making two nested for loops, the outer one for the rows of your matrix and the inner for the columns. The "index variables" of these loops come from the temperature and wind ranges, so they might be named temp and vel. now these two loops will create the 192 values you need, and the job is to put each in the right location (as the element at the proper two indices). Use two new local variables, row and col, starting at 0. They will count the number of times you've been through the row loop, and (RESET to 0 for each row!) the number of times thru the column loop. Thus they will give you the (1,1)....(9.8)....(16,12) indices you need to express where to store the chill factor you computed in the inner loop.
Don't forget the comments.

Read the Root-finding
tutorial, write Newton and secant method root-finders, and
use each of them to find the root of
Coding hints: For these one-off sorts of problems it makes sense to have the newton or secant function in a .m file, followed by two sub-functions evaluating f(s) and f'(x). Then to compare the same problems, you can cut and paste the Newton and secant functions on top of the sub-functions, or the sub-functions under the root-finders, and everything's always all together in one file you can call from the command window with one line.
Under no circumstances save all your successive values of x in a vector! Just because we use subscripts to identify them does not mean you must remember them all: save one for Newton, two for Secant!
Note: If you want to provide a user with a general
root-finder, you'd like to provide him with a way to pass
the
See Attaway Ed. 1: 11.1.3-11.1.4. Ed 2: 12.1.3-12.1-5 or our matrix tutorial.
Write a function my_transpose() with prototype
Your function takes a matrix as argument and returns its transpose. To transpose a matrix, swap its rows and columns: The ith column of the transpose M' of a matrix M is the ith row of M. (Hint: this meansfunction trans = my_transpose(mat)
Hint: A common programming construct for processing (2D) arrays and matrices
is to nest two loops: An outer one going through the rows and an inner one
that goes through the columns for each row.
(Or the outer one goes through the columns, and the inner one through the
rows.) Inside you do something at each array position.
Code outline would look as follows.
% Initialize arrays matrixA, matrixB ...for row = 1 : nrows % maybe some setup for processing each rowfor col = 1: ncols % do something with matrixA(row, col), matrixB(row, col), ...end end
Test your transpose on various random matrices of various sizes (including single row and column). Test by comparing my_transpose(X) with Matlab's built-in X'.
See Attaway Ed. 1: 11.1.3-11.1.4. Ed 2: 12.1.3-12.1-5 or our matrix tutorial.
Write a function mat_prod() with prototype
The matrix product C of matrices A, B is defined by
C(i,j) = ∑k A(i,k)B(k,j). Thus the number of
columns of A must be equal to the number of rows of B.
Your function mat_prod()
takes matrices A and B as arguments and returns their product
or writes an error message and returns 0 if A and B cannot be
multiplied. Use three nested for-loops.
Hint: The first thing your function should do is to check that the sizes of the input matrices, A and B are compatible for multiplication. Then you can figure out the number of rows and columns that the output matrix C will have.
Another hint: the loop that changes k is the 'innermost loop'. Fact: each element of the product matrix is a dot product of a row of A with a column of B, so you're also computing dot products as a side effect.
WARNING: DO NOT use any built in matrix (or vector) multiplication commands or : ranges. No credit if you do. The idea here is to figure out how to do it yourself using only basic programming constructs. However, you should use Matlab's * operator to compare your answer with a trusted one.
Expand your answer to Attaway's Question 4.14,
above, to return both the mean
and standard deviation of the elements in an N-vector
of numbers. Use the prototype
function [average, std_dev] = mean_std(X)
Use the "statistical" (normalized by N-1) definition of
variance given in Attaway 12.1.2. Of course you won't use built-in
mean, std, var. See the "Loops" lecture notes for introduction
to mean and standard deviation, or try Wikipedia, etc.
Test your results on matrices of zeroes, ones, and rand's, that is uniformly distributed numbers between 0 and 1 generated by something like Data = rand(N,1), comparing your results with calling matlab's built-ins mean(), std() for a few different sizes of N, including 1.
Look up (Wikipedia's good) the formulas for the mean and variance of a uniform
continuous distribution. Run your mean_std() function from the last
Problem for rand(N) matrices for
N = [2, 10, 20, 40, 80, 160, 320] and
save the results in a vector.
Plot the results on two graphs (one for mean, one for std.)
Use Matlab's figure command to give you two plot windows.
What can you say about the results you plot, given what you expect
from the formulas?
Programming Assignment 5
(Code and Readme: 100%, Writeup 0%)
See the Working Directory section in Assignment 1. Arrangements same as Prog. Asst. 3 and 4 above, except extra credit is not available, though extra problems are available for practice. These questions often call for a script that calls a function. Your main.m script is just the concatenation of all those called-for scripts, with subscripts for individual problems adequately labelled of course.
Attaway
Chapter 2: Questions 9, 16*, 17,19, 30, 32*, 34. (Plotting)
Notes: Ch2. Q16, 17, and 19. Plotting is very important for future assignments. It is often how we engineers report our results. Be sure you are comfortable with the plot command and get help if you have questions. Attaway Ed. 1 Ch.10 ( = Ed.2 Ch.11) could be useful too.
Q 2.32: Slight misprint here -- the square-root should include the entire product 2π n, and that square root is followed by the exponentiated fraction. Here π is 3.14259..., for which you may use matlab's pi, and e is the base of natural logarithms; e = 2.71828.... , and it's not a predefined Matlab constant, sorry. Check out exp(). Matlab has a built-in function factorial(N) that you can use to check that your approximation is reasonable.
What We Learn Below: Some values can only be calculated by series approximations, which can converge to their answer at different rates. Some system behaviors are complex enough that they can only be computationally approximated, by simulating the system and nature's randomness (if the system has "random" components best described statistically, like weather or how many cars arrive at a turnpike booth per hour).
You know π is a transcendental number, that is it has no
closed-form mathematical formula.
Recall that a common programming idea is the accumulator approximation,
which sums or multiplies some number of terms from an infinite series
(see Attaway 4.1.1).
As a programer you need to map the pattern of terms in the series into
an expression that gets added or multiplied into the term that is
accumulating the answer. Simple example: you can add the first 10 multiples
of 7 with
sum = 0; % initialize sum to 0 for i = 1:10 sum = sum + i*7; end;After the loop exits, your sum will be in sum.
Infinite series are vitally important practical approximations that occur throughout engineering. They are also potentially quite beautiful and surprising just as mathematical objects. Certain series (like converging geometric series) are both common and easy to solve in closed form by a very simple formula.
The Leibniz formula for π is an alternating sum:
π = 4/1 -4/3+ 4/5 - 4/7+4/9 - ...
For a simple 2-line proof, go to the fount of all knowledge.
Write a function with the prototype
function my_pi = Leibniz(N),
which returns an N-long vector with my_pi(j) being the
result of summing the first j terms of the Leibniz formula.
In a script or in the command window, run it for N = 22 and keep the
result. Make a 22-vector whose every element = pi, and
subtract your result vector from your π vector to get an error
vector, and plot the error (versus i, but you don't have to
say so).
The Newton formula is
based on a series approximation to arcsin(1/2).
π/6 = 1/2 +
[ (1) / (2) ] / (2^3 * 3) +
[ (1*3) / (2*4) ] / (2^5 * 5) +
[ (1*3*5) / (2*4*6) ] / (2^7 * 7) + ...
Here it looks like you want to use ^, and maybe write a factorial-like subfunction or two to compute those products. You can get away with that here, but for one thing it's a bit of trouble and either adds loops or more functions into the mix. It also computes each term as if you haven't done any work so far, which is wasteful and can sometimes lead to numerical errors. Here it's inefficient but numerically harmless (CB tried it both ways). It's always better style and often yields better results to use previous work (the previous term, say), to calculate a term. Here CB kept two variables to be updated every time around the loop. One for the value of the numerator of the previous term and other for the value of the power of two in the denominator of the previous term. From them it's easy to calculate the current term.
Remembering Newton's formula gives π/6,
Write a function with the prototype
function my_pi = Newton(N),
which returns an N-long vector with my_pi(j) being the
result of summing the first j values of π calculated
with Newton's formula.
In a script or in the command window, run it for N = 22 and keep the
result. Print out this result and look at the terms: they are
converging at about the rate of one digit per iteration. Compare
with the Leibniz vector of π approximations. As with Leibniz,
Make a 22-vector whose every element = pi,
subtract your Newton result vector from your π vector and plot the
resulting error vector. Using hold on, display your Leibniz
and
Newton error vectors on the
same plot. Conclusions?
One obvious conclusion is that the Newton error is falling off so fast that much of the plot is uselessly close to zero. If we're right about the one-digit-per-iteration observation from the last paragraph, we'd expect the error to be falling exponentially (about a factor of 10 each iteration), so its logarithm should be in a straight line. So we are definitely motivated to plot the logarithm of the error. You should see a straightish line (note the log gets more negative as the fraction gets smaller). Or does anything seem amiss?
If so, display the whole 22-long error vector. Is the last entry negative? (CB's was.) If so, you get a complex logarithm for that element, which probably means Matlab converts the whole array into complex numbers and then seems to pick the imaginary component to show us, or something else mysterious. Anyway, that negative error is a sure sign (hyuk, hyuk) we are butting up against the limits of numerical accuracy in the machine, since mathematically this formula always underestimates the true value.
Fixes: Most honest is to delete the last element and deal with a 21-long vector. Quick fix would be to take the log of the absolute value of the 22-long vector, even though the last entry could be meaningless. Also clearly we're not going to gain anything from more iterations than 22 for Newton, which isn't true for Leibniz.

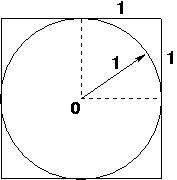
We'll simulate throwing darts randomly (importantly, randomly with a uniform distribution) at a target that looks like the upper-right quarter in the diagram. We'll count how many wind up inside and how many we threw in total, and the ratio of inside/total will be approximately π/4. Statistically, the ratio approaches the right answer more closely as the total number of trials (dart tosses) increases.
Above, the area of the square is 4 and the area of the circle is π. Or, the square area above and right of the dotted lines is 1 and the area within that square area occupied by points inside the quarter-circle is π/4. That's the key insight. Also important: Since the formula for a circle is x2 + y2 = r2, we see that if you give me an (x,y) point I can tell you if it's in the circle (or quarter circle) or not: if x2 + y2 ≤ 1 then it is, else it isn't. Also, rand() returns uniformly-distributed random numbers between 0 and 1. We're almost ready to roll: we suspect we may have to throw lots and lots of darts to get a good estimate, so we'll compute a sane-sized vector of π estimates by throwing a whole volley of darts (size TBD) between each.
Write a function with the prototype
function my_pi = Monte_Carlo(N,volley),
which
which returns an N-long vector with my_pi(j) being the
π estimate from throwing j*volley darts. The function
keeps two variables, total_darts and in_darts, for number of
darts thrown, and the number that landed in the
quarter-disk 'pie slice' inscribed in a square of side 1. It has a
doubly-nested for-loop (outer varies from 1:N, inner from 1:volley),
which saves the result (in the outer loop)
after every
volley-
long volley of darts has been thrown (in the inner loop).
There are N volleys.
In the inner loop, we generate a random x in [0,1] and a similar y, add 1 to total_darts, and add 1 to in_darts if x*x + y*y ≤ 1.
As before, plot the error of the estimates. The volleys may have to be pretty big to get a good approximation with N = 22.
A prime number is only divisible by 1 and itself (so 2 is the only even prime). Now it should be clear that if some number N has an integer divisor (called a factor) that is greater than sqrt(N) then it must have another factor that is smaller than sqrt(N), since if all its factors are greater than sqrt(N) every pair of them would multiply to give a number bigger than N. So to prove a number is not prime, we need only find a factor that is smaller than or equal to its square root. (Aha! The Matlab functions rem() or mod would be useful here.)
Part I.
Write a function a_factor = has_factor(N)
that returns a factor (the first one it finds!) such that
the argument is evenly divided by that factor (should such a factor exist)
and returns 0 if a factor does not exist (N is prime).
My function's 7 lines long, calls sqrt() and has a for-loop that
contains an if and a (conditional) return.
My for-loop starts for poss_fac = [2, 3:2:s]
What's going on here and what is s? To get started, what values does
poss_fac attain? (hint: 2, 3, 5, 7,...,s).
Your loop could be different and still work, of course.
If you understand why mine works, feel free to use it without attribution.
Part II.
This part is totally independent of Part I. They are completely
different algorithms for finding primes, but both are based on
the same simple theory. Rather more interesting primality tests,
used for instance in modern cryptography for testing primality of
humongously gigantic numbers, are described in Wikipedia's
Primality Test
article or any introductory cryptography text written after 1984.
Theory: From the definition of prime, If a number has a factor it has a prime factor, since if the first factor F isn't prime then F has factors itself, which are getting smaller and eventually must be prime. So if we started with the integers and the smallest prime 2, then repeatedly deleted all multiples of the current prime P and took the smallest survivor bigger than P as the new current prime, you'd see something like
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25...
1 2 3 * 5 * 7 * 9 * 11 * 13 * 15 * 17 * 19 * 21 * 23 * 25...2s
1 2 3 * 5 * 7 * * * 11 * 13 * * * 17 * 19 * * * 23 * 25...3s
1 2 3 * 5 * 7 * * * 11 * 13 * * * 17 * 19 * * * 23 * *...5s
and we've deleted all numbers with factors (here up to 5), and thus have left all primes up through 25 since 52 is 25. Notice that we don't need to know any primes except 2 to start! After we delete every 2nd entry, the next survivor (3) is the next prime, so we need to delete every 3rd entry. Next survivor is 5, the next prime, so we delete every fifth...etc.
Write a function prime_vec = eratosthenes(N), which uses the above "Sieve of Eratosthenes" idea to produce a vector of all primes between 1 and N. That is, it produces a vector as above, with primes and non-primes (maybe set non-primes to 0?), THEN squeezes out all the non-primes so you get back a vector whose ith element is the ith prime. Nice animation of the sieving (not the squeezing) process in Wikipedia's Sieve Article.
Don't forget to comment your code and use meaningful identifiers. Also, if things seem to get complicated, you're making the problem too hard or haven't found the highest-leverage Matlab commands.
See the Universal Hand-In Page .