
MatLab as a Calculator
Daily Quibble Question:
What is the 4th root of 1?
Announcements
Labs Begin Tonight (there are two).
For class today, get to this here web page
(http://www.cs.rochester.edu/u/www/u/brown/160/lectures/2CalcOheads.html)
Textbook Features
- Table of Contents
- Index
- Key Words
- Explanations and Examples
- Quick Question!s
- Practices
- Summary
- Programming Style Guidelines
- Matlab functions and commands
- Matlab Operators
- Exercises
Where did the lectures come from? Working straight through the
text, while leaving some things out (and adding a few things).
Moral: the text is your friend.
Once and Future Lectures
In-class portion of this course is somewhat
"old style": with lecture component and "powerpoint."
Isn't optimal for learning a lot of things.
Especially not the way to teach programming
languages, any more than soccer or piano performance. Hence the
lab sections, which are smaller groups, more interactive.
Individually: Sit down with the manual in your lap, and work
bigger and bigger problems. Read code from places or people you
respect. Find forums for advanced questions. You'll know more than
most professors in a month.
Still, we have these big lectures, the goal of which is to give you
an overview/introduction to what you will be learning through your
individual efforts on the assignments.
The lab sections are your forum for getting more individually
directed guidance.
We should be able to use all this computer technology that
is sitting in front of each of you to increase lecture effectiveness.
We're still experimenting, so bear with us...
For example, you can scan back and forth through the lecture notes
without asking the prof to go back a slide.
Useful or distracting?
Individually, reading book, notes, other materials before class is a
REALLY good idea,
1-2 hours/class outside study a good investment.
Believe me, what the prof says will make a lot more sense.
MatLab
- Matlab is an application program. Versions for Windows, MacOS,
Linux, etc.
- Basically it is a sort of super-calculator that you interact
with by typing commands.
- It comes with a whole lot of pre-existing commands, mostly to do
things with numbers and arrays of numbers.
- As part of its super-abilities, you can write programs by putting
together existing commands, which can then be saved and
used as new commands.
- The programming method is "complete" in that anything that can
be programmed for any computer in any language can be programmed
using MatLab (modulo symbolic I/O).
- For a complete programming system, it is relatively easy to use,
and IS widely used among scientists and engineers.
- Hardware/software extension packages can be used to access
peripheral devices from within Matlab, thus it is somewhat
useful as a general-purpose control environment,
though not a serious one as it lacks usable real-time and
parallel-process management primitives.
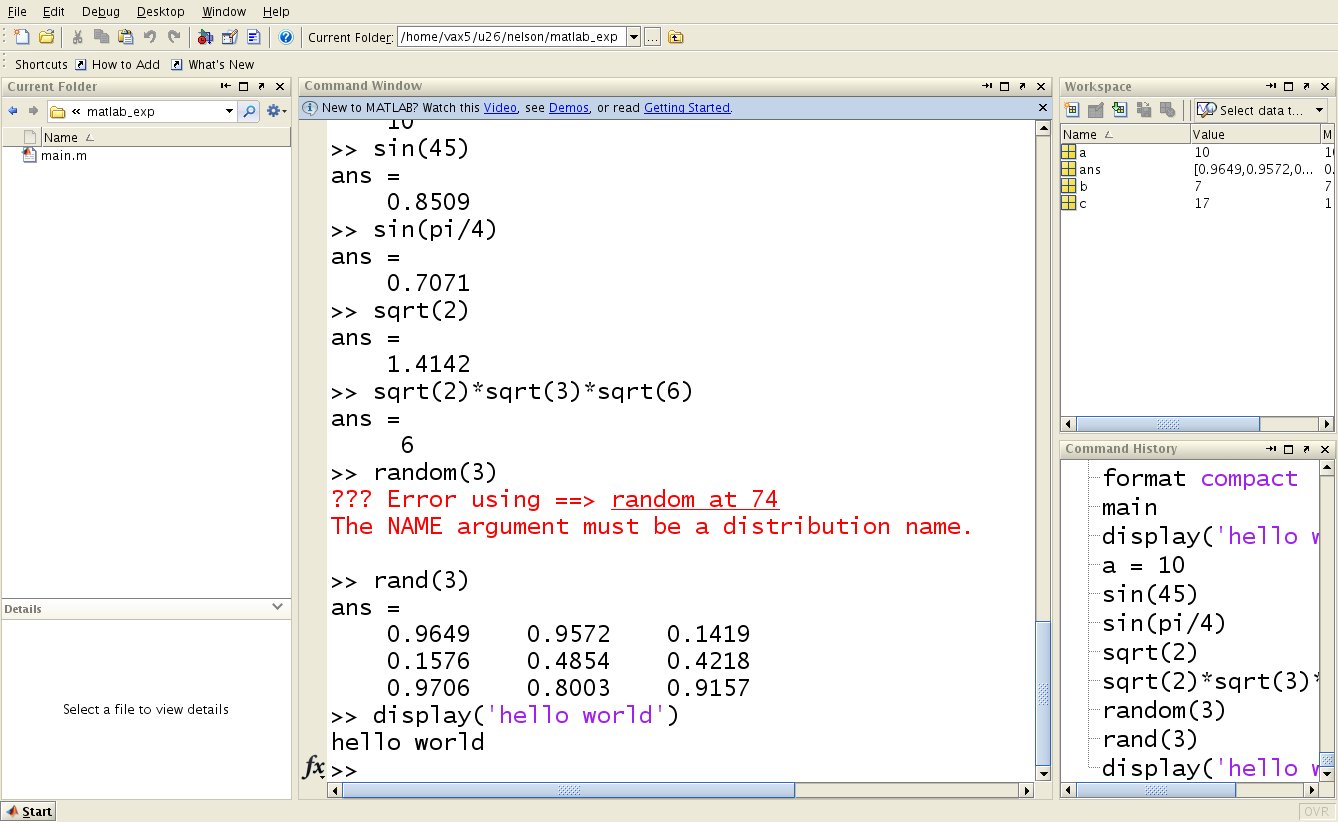
MatLab Workspace (Attaway 1.1)
To start MatLab, double-click its Icon (Windows, MacOS) or type
"matlab" to a command-line interface (Linux).
A main window with familiar generic GUI menus and several subwindows
will come up. This is your playground.
- Command Window -- you type commands here
(help, Function List Icon, function 'completion')
- command history window
- workspace (variables) window
- current directory window
- editor window (comes up as a separate window)
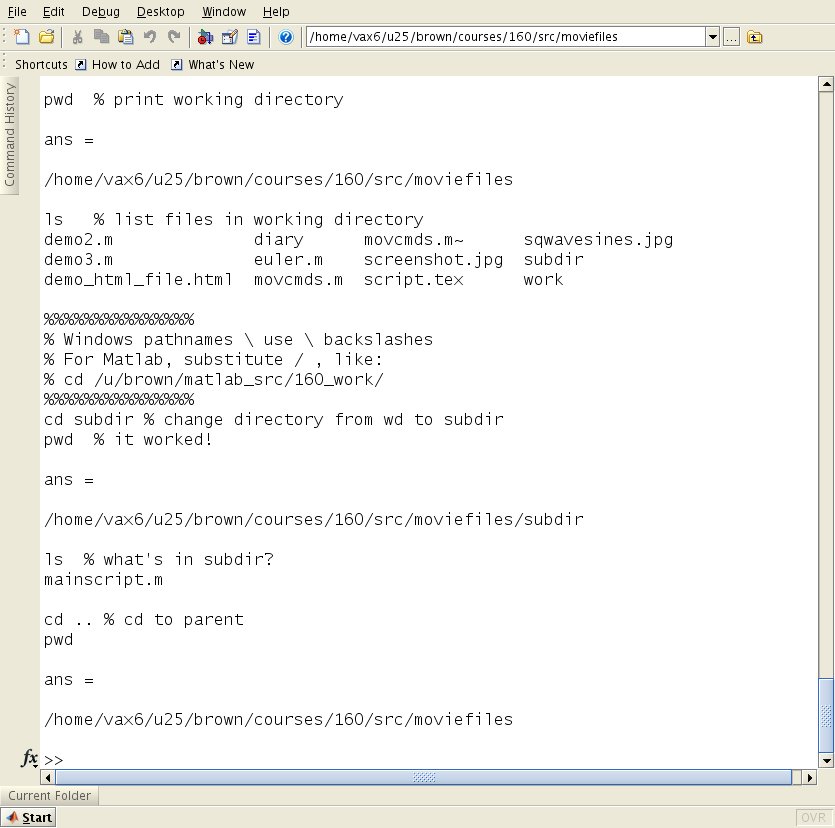
Directory-changing commands
It is important to know what directory Matlab is using.
This is essentially where it lives. Use
>> pwd
to find out. We highly recommend on UR Laboratory machines
that you be in
C:\testing\Documents\MATLAB\
since very mysterious errors can happen if you're not.
Store zip drive to this directory and reload zip
from that directory. Matlab saves files
and changes into this directory if you start there.
If you're NOT in this directory, go there with
>> cd C:/testing/Documents/MATLAB/
Using backslashes like
>> cd C:\testing\Documents\MATLAB
might work too.
Demos
Data Types (Attaway 1.2)
MatLab, Other Languages Have Data Types
- integers
- floats
- logical (boolean): true, false
- complex
- vectors (row and column)
- arrays (1,2, 3,... dimensional)
- strings
Demos 2
Variables, Operations (Attaway 1.2)
A variable is a name for a reserved box into which you can put
values: (number, matrix, string, ...).
Think of it as a labled slot or drawer.
Variables often hold
intermediate values: essentially short-term memory used in computations.
We say we "store" values into a variable. Mentioning the variable's
name
"retrieves" its value. We also say a variable evaluates to its
value
>> Partial_sum = 39;
>> Partial_sum
Partial_sum =
39
Variable Names: Case sensitive strings of letters and numbers,
can be fairly long (good), can't start with a digit, including
underbar is ok and useful for readability.
Legal:
Final_value , MeanTemperature , x ,
Room_203 , y67x43 .
Illegal:
123XYZ , my-long-variable ,
this!hurts , (*&^-it .
Variables may be
assigned (bound) , or
unassigned (unbound) .
An assigned variable has a value.
Operations on data types include:
=,+,-,* (times),/, and
^(power).
Assignment =, is NOT mathematical equality.
It means: "assign value of expression on RHS to variable on LHS".
Some languages write < -- for assignment:
Demos 3
Expressions ( Attaway 1.3)
An expression is a "grammatical" combination of
already-defined
constants, variables, function calls, operators, and parentheses,
that has a well-defined value.
There are String Expressions, Numerical Expressions, etc. depending on
the value produced.
In the command window, typing an expression w/o a terminal ;
causes it to be evaluated,
and the resulting value (the "answer") printed to the screen.
Can also assign value to a variable with =, w/ or w/o printing, e.g.,
Quadratic_Discriminant = b^2 - 4*a*c;
Use the matlab command window to evaluate 7 to the third power.
See results
In Matlab, "carriage returns" are important.
To continue an expression on a new line ellipses (...) must
be used, e.g.,
long_expr = a+b+c+d ...
+e + f + g
Demos 4
More Expression Details (Attaway 1.3 Cont.)
Assignment to an unbound variable is sometimes called initialization.
Addition or subtraction of a fixed quantity (often 1) is an
increment or decrement to a numeric variable.
Such incrementing and decrementing is an important concept:
incrementing array indices moves through the indices and allows the same
operation to be applied to every element of an array.
More operations: / is divided by, \ is divided into
i.e., 1/4 is the same as 4\1.
You may find this confusing, or useful.
The order in which operations are performed when evaluating
expressions is controlled by operator precedence and parentheses.
Precedence is as follows, from highest to lowest.
(),^, - (unary),*,/,
\,+,-,
and from left to right.
Thus 2+x*y^3 is implicitly parenthesized as
(2+(x*(y^3))),
and a+b-c as ((a+b)-c)
Built-in Functions:
Lots of them, (klik the Fn list in lowerleft corner of command window)
also try help and the
Fn-''completer''.
E.g. Calculator-like fns:
sqrt(),
sin(),
tanh(),
abs(),
rem(),
gcd(),
bessel(),
...ad infinitum
Demos 5
Yet More Expressions Details (Attaway 1.3 Cont.)
Functions ABOUT Variables
- who
- whos
- clear
- clear foo
- Tests like isNaN(), isinf()
Useful built-in constants (pre-defined unchangeable variables)
pi,
i, j,
inf,
NaN, eps.
Predefined variables kept up to date by system:
clock, date, ans.
Demos 6
Numerical Data Types (Attaway 1.3 Cont.)
For us, mostly floats (aka reals),
possibly complex: single and double (precision).
Logarithmic idea of floating point representation:
sign bit, some bits for exponent, some for mantissa.
name s eeeeeee mmmmmmmmmm
single 1 8...... 23
double 1 11..... 52
Default is double precision.
There are also integers:
int8 (byte)
int16 (short)
int32 (word)
int64 (doubleword)
Numeric variables have definite ranges. Try
intmin('int64'), intmax,
realmin...
For example, realmax('double') yields 1.7977 e +308 (!)
Also logicals false (0), true (1),
with nonzero being interpreted as (and automatically sometimes converted to)
1 for logical uses. Total chaos, IMO:
MatLab is loosely typed in the sense that it tries to make sense out of
whatever you have entered, and converts from one type to another
if needed, without fussing about it (or telling you).
Usually it does the "right" thing.
Some languages are strongly typed and generate an error if you
mix types in an expression without explicit conversion.
Some languages have a few rules for implicit conversion, and may
fuss otherwise, or silently fail in a mysterious fashion
(notoriously, C, C++).
Demos 7
"The" Matlab Data Type: Matrices (Attaway 1.5)
NxM Matrices , 1xM row vectors, Nx1 column vectors (all are 'arrays')
of elements. Real is a 1 x 1 matrix. There are multi-dimensional
arrays as well, either just as data structure or there is also (of
course) a tensor toolbox.
Typically, Matlab is "like, whatever.." about matrix-creation syntax:
some_vec = [1.5 2.4 3.5];
row_vec = [2,4,6,8];
col_vec = [-1.3; 4.5; 100; .00001];
square_mat= [
1 2 3
4 5 6
7 8 9];
same_sq_mat = [1 2 3; 4 5 6; 7 8 9];
The 'colon', 'range', or 'iterator' operator
--- 1:N increments from 1 to N by default 1
start:increment:end increments from start by inc to end.
linspace(first, last, howmany)
creates a vector of evenly-spaced values.
OK_vec1 = 1:5;
OK_vec2 = 10:-2:-4
OK_vec3 = linspace(0,10,4) % careful! 2.5 not included!
Mathematical operator transpose() or '
swaps ith row with ith column for
all rows.
col_vec = transpose(row_vec);
matrix_transpose = matrix';
Useful initial matrices can be created by
created by:
- zeros(n) not "zeroes": an nxn square matrix of 0s
- zeros(n,m) an n x m matrix of 0s
- zeros(size(arr))
- ones(...) matrices of all ones
- eye(n) matlab (or Wash DC) for I: nxn identity matrix.
- eye(n,m) I-like matrix of dubious utility
- rand(n) nxn matrix of random reals 0.0 - 1.0
- magic(n) a magic square (!).
Demos 8
Pushing the Matrix Envelope
Attaway 1.5
Concatenation of arrays, vectors.
If A is [1,2,3] and B is [4,5,6], then
[A,B] is the row vector
[1,2,3,4,5,6], and
[A;B] is the 2 x 3 matrix
[1,2,3]
[4,5,6]
As a general rule: operations and function calls extend to arrays:
e.g + and - work for vector-matrix addition, and
function calls such as
abs([2 3 -4]), sqrt([2 3 -4]) etc.
work as you might expect on an element-by-element basis.
Other non-mathematical transformations include:
fliplr(),
flipud(),
flipdim(X, dim),
rot90(X) or
rot90(X, ntimes).
Also extension: e.g.
x = [1, 2, 3]; % x is 3-elt vector
x(6) = 10; % not so fast!!
[1 2 3 0 0 10]; % so much for 'bounds-checking'
Extension is not only weird and confusing, it's inefficient:
try to preallocate vectors and arrays in the proper size (or larger).
Fore example, use
new_mat = zeros(M,N)
Demos 9
Array Indexing (Attaway 1.5 Cont.)
Indices are used for accessing and updating array values:
x = zeros(1,3); % need both arguments to get row
Y = zeros(3,1); % or column vector
x(1) = pi; % but only one argument to index it!
Y(2) = pi*sqrt(2);
n=3;
x(n) = x(1);
Y(n) = x(n);
Array indices start with 1 in Matlab (and old versions of Fortran)
rather than with 0 as in C, C++.
Also (since an index can surely be an array !!)
x([1 3 2]) is [x(1), x(3), x(2)].
Recall: the (colon, range or iterator) operator.
This can be useful for specifying
subsets of array indices
x = [1:4;2:5] % a 2 x 4 matrix
x(:,1) % everything in column 1 -- a column vector
x(2,:) % everything in row 2 -- a row vector
x(:,2:3) % everything in columns 2 and 3 -- a 2x2 matrix
The empty vector [] has length 0.
It can be accessed or updated,
concatenated, extended, and assigned (to
rows, cols, submatrices, thus removing them).
Such notation can be compact, but can also be confusing.
Can't remove individual array elements or subsets of
rows, since all rows must have same length, as must cols.
x = [1:4;2:5]
x(:,2) = []; % remove column 2
x(5,5) = 7; % extend the matrix to size 5x5,
unpecified locations are 0
y = [1,2,3; 4,5,6; 7,8,9];
y(1:2,[1 3]) = [20 21;22 23];
% yikes... but 2x2 replaced w/ 2x2...
y(1:2,1:2) = pi; % works too.
In general, we don't recommend such tricks, unless fully commented,
and intent is very clear.
Demos 10
Dimensions and Sizes (Attaway 1.5 Cont.)
Rows and Columns are 1st and 2nd dimensions of 2D arrays.
More generally we can have 1st, 2nd, 3rd... dimensions.
It's easy to exceed MatLab's capabilities if you use more than a
few dimensions --
How many elements would be created by
>> A = zeros(100, 100, 100, 100, 100)?
See results
size(A), returns a 1xn vector giving the extent of each dimension
in an n-dimensional array A.
Thus if A is a matrix, it returns [nrows, ncols].
Note!
size(vec) returns [1, length(vec)] for a row vector and
[length(vec), 1] for a column vector because Matlab interprets the
vectors as matrices by default.
Surprised?!!.
length(vec)
returns the number of elements in a vector.
To get the total number of elements in any array,
use numel(A).
The end function used as an array index
for a dimension returns the highest value of the subscript in the
dimension, as in x(5:end, 7:end),
y(end, end)
(which extracts the lower, right-hand part of a matrix)..
Note that Multiple-return-value functions can be handled in
matlab by returning a vector, as the function size()
illustrates.
Demos 11
Random Numbers and Matrices (Attaway 1.5 cont.)
Random numbers very useful in practical programming, especially for
simulations and testing.
MatLab provides
many choices of random distributions, (uniform, normal (gaussian),
poisson...)
help random
There are also easy-to-use defaults and specializations:
e.g., rand(), randi()
(not randint), randn().
rand(2)
ans=
0.8147 0.1270
0.9058 0.9134
Demos 12
Next Time and Until Further Notice
Bring Attaway to Class...we'll use it.

Last update: 04/22/2011: RN



