
Disjoint Sets
Weiss Ch. 8
You're too young to have lived through "New Math", though you may know
Tom Lehrer's
Song. Sets are an important practical and mathematical concept
and operations like union, intersection, difference come into all
sorts of practical applications like Constructive Solid Geometry
expression trees for graphics, database boolean queries, image
analysis, graph theory, compilers with types, etc.
See our PPT for a nice visual set union algorithm for discovering
connected regions in an image with a "scan-line" algorithm, after
which we can tell which disjoint region (set) an individual picture
element (pixel) is in.
There is a very simple (to program) but hard (to analyze) representation for
sets to support the union-find functionality.
Equivalence Relations
Our sets are collections of elements from some domain (integers,
employee records,..)
defined by an equivalence relation that states which
elements in the domain are "the same".
Notoriously, "a relation is a set of ordered pairs." You probably
thought a relation was something like "before", "father-of", or
"greater than".
A relation R (like "greater") is defined on a set S if for every pair
of elements (x,y) in S the relation is either true or false. If it's
true, then we say "x is related to y", so we can
map the formal definition and the intuition onto each other. So the
ordered pairs (x,y) for which xRy is true (say "x happens before y")
defines the (ordered pairs in the) (say "before") relation.
An equivalence relation R satisfies
- aRa for all a ∈ S (Reflexivity)
- aRb ⇔ bRa (Symmetry)
- aRb and bRc ⇒ aRc (Transitivity)
E.g. > isn't an equivalence reln: not reflexive or symmetric. ≥
is not symmetric. If love had any of the three properties there'd be
a lot less literature. For triangles, similarity is an eq. reln;
for people, "have same name day" is; for numbers "congruent mod n"
and
"equal to" are.
Dynamic Equivalence Problem
How decide if aRb for some equivalence relation
R in the (usual) absence of the "set of
ordered pairs" that abstractly define the relation? Suppose we have a
four element set {a,b,c,d} and we know aRc, cRb, dRa, bRd?
So is aRd? (quickly, now!).
Given an equivalence relation on S, the equivalence class of an
element is the subset of all elements equivalent to it. These classes
"partition" S (they are disjoint, since if any element were
shared between sets transitivity would make the sets the same.)
Given this situation, the find operation finds the name of the
equivalence class (set) of an element. The union operation
"adds relations", or evaluates to the (set-theoretic) union of the sets if they are not
identical already (takes two finds to check this). Union destroys its original arguments and
maintains mutual disjointness. Hence the "disjoint set union/find
algorithm".
Our sets change as we do operations, so the algorithm is dynamic.
It is
'online': in a series of unions and finds, the result of each are
returned before the next is calculated.
You can
imagine a batch or off-line algorithm that takes a series of unions
and finds and spits out answers having seen the whole series. Even a
parallel
algorithm...?
We don't care about what the elements are "like" (e.g. their
values). They can be represented integers 0...N-1 resulting maybe from
a hash calculation. Likewise we care not about the "name" of a set:
we just need find(a) = find(b) if aRb.
Dang! Can do union or find in constant worst-case time, but
not both. We're going to be interested in the running time of a
sequence of union and find operations: the length of that sequence is
the length of our "input."
Find is Fast
Keep the name of its equivalence class in an array indexed by
element. O(1).
But union involves scanning N-long arrays and maybe creating an O(N)
one. So Θ(N), or to do the maximum possible number of unions
(N-1),
Θ(N2), which is too slow if the application has
fewer than N2 finds.
If equivalence classes are linked lists, they can be unioned in O(1)
time but it is still possible to have to do N2 name updates over
the course of many unions.
Keeping size of equivalence classes and in a union changing name of
smaller to the larger gives O(NlogN) time for N-1 unions (each elt
can have its eq. class changed only logN times). So M finds, N-1
unions
means O(M+NlogN) time with this latest implementation.
Union is Fast
We show a union/find algorithm with M finds and N -1 unions in
slightly more than O(N+M) time.
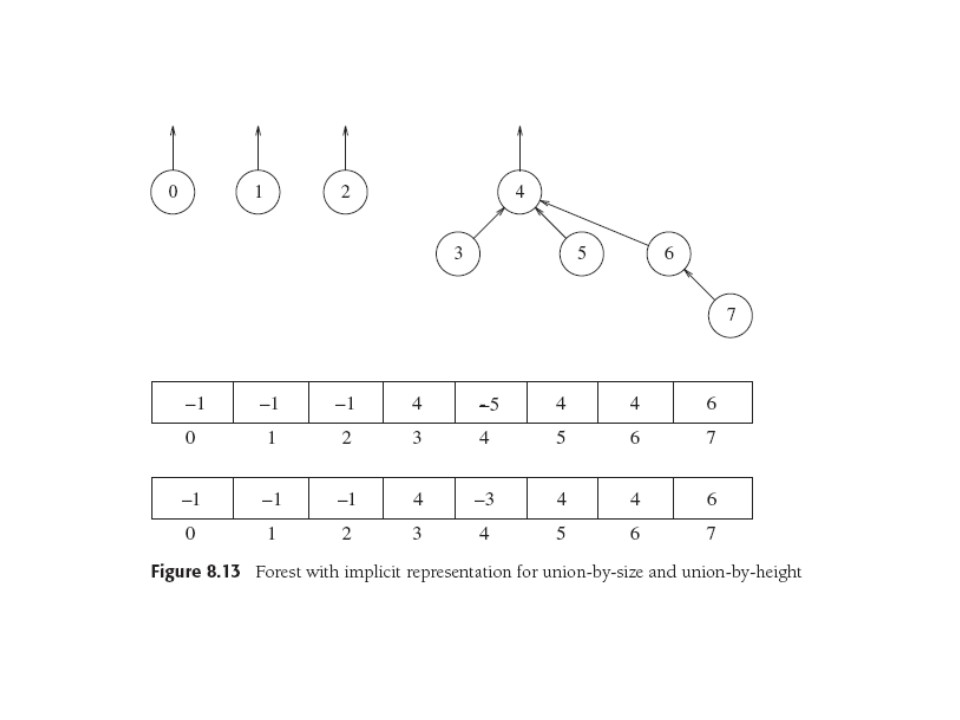
Sets will be trees and one's name is the name of its root. The domain
is
a "forest" of trees, and we imagine each set initially to be a
singleton. We only need links to parents. Here we start with 8
elements and union (4,5), (6,7), and (4,6) in that order.
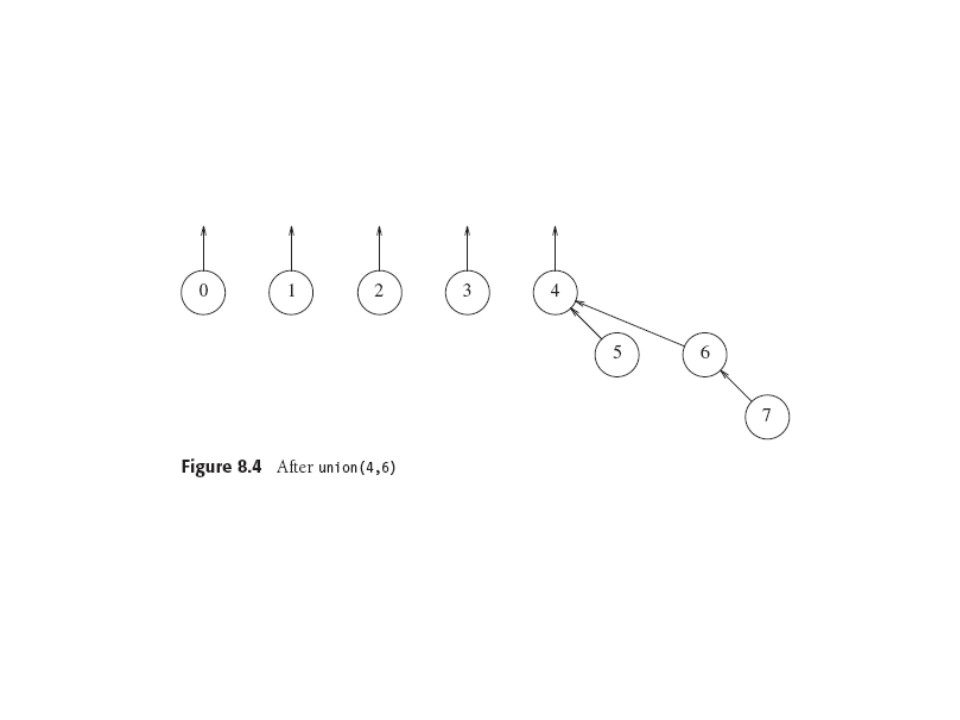
A simple array representation has an array s whose indices are set
elements i, with s[i] = -1 if i is a root, else s[i] = parent of i.

Class definition, initialization, union and find are all trivial to
write
(ignoring efficiency). Average-case complexity depends on the
definition of 'average', and three different models of that lead to
Θ(M), Θ(MlogN), and Θ(MN) for M finds, (N-1) Unions.
Smart Union Operations
As usual, we're looking for shallow trees.
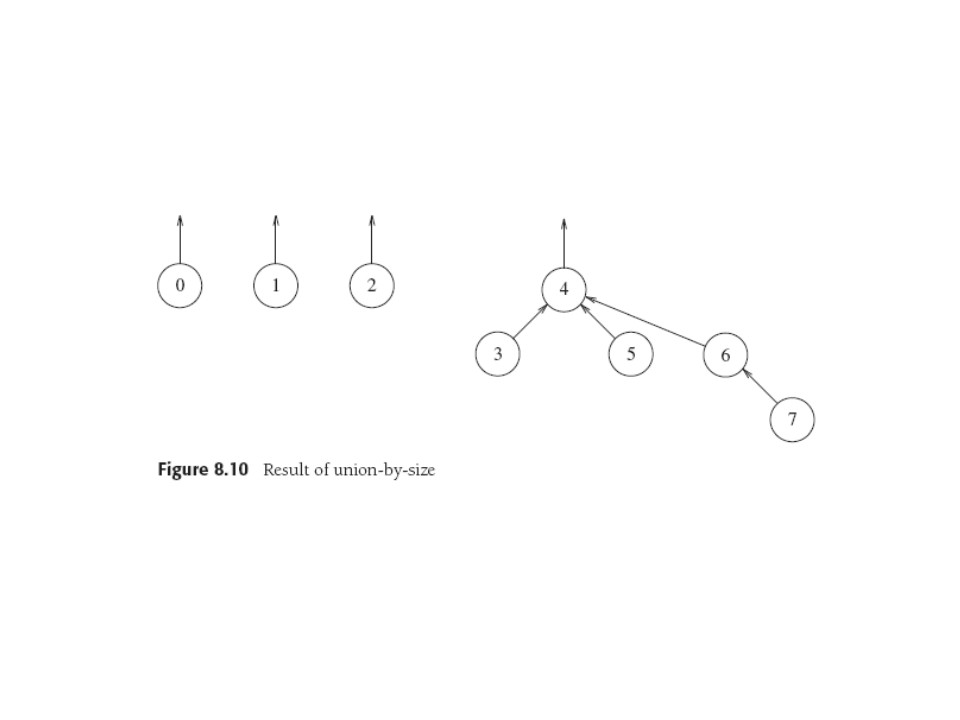
Union by size always makes the smaller tree a subtree of the
larger.
So union-by-size(3,4) puts the small 3 under the large 4 tree in the
last forest:
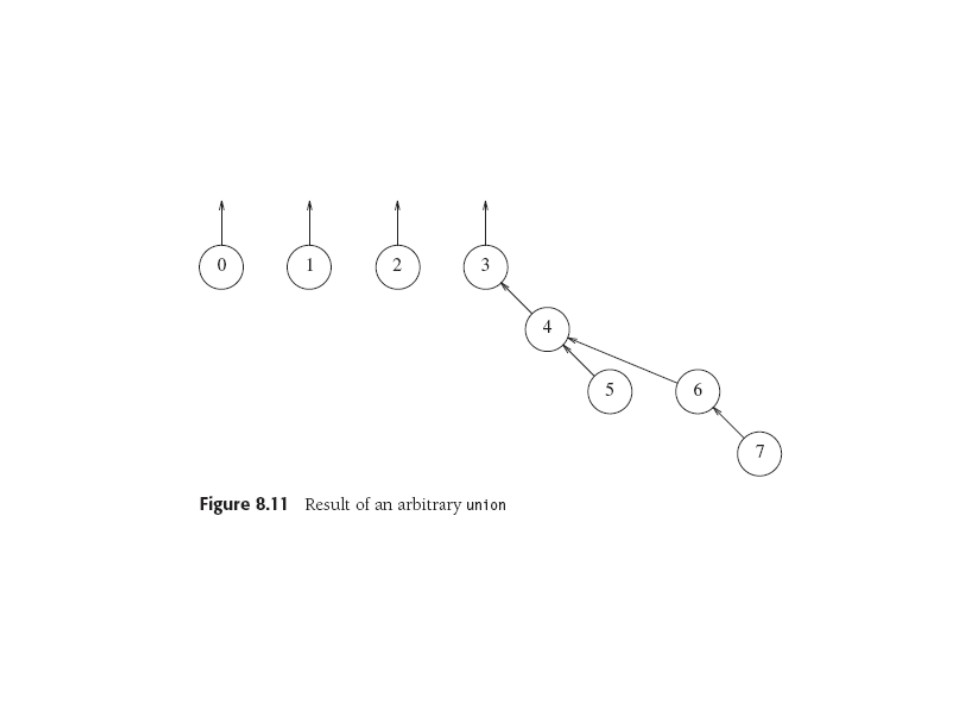
But union(3,4) performed (arg2 under arg1) as before yields the deeper
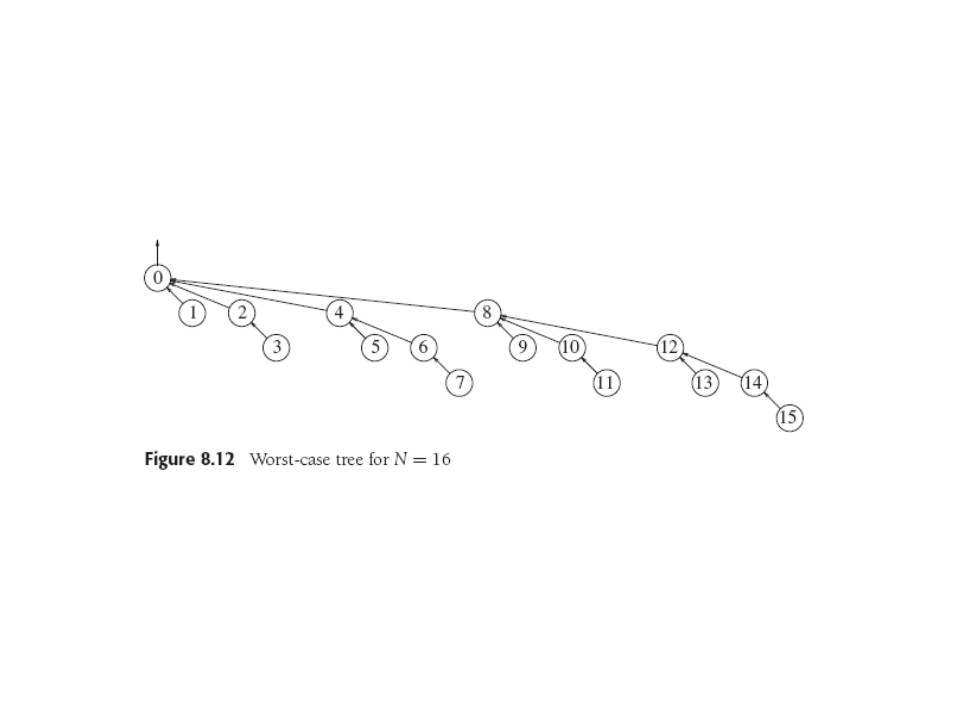
Union by size yields trees of depth ≤ logN. Proof: every node
starts at depth 0, and its depth increases only by a union producing a
tree at least twice as large as before, which can be done only logN
times.
Corollary: M finds take O(MlogN).
The worst depth is produced if all unions are between equal size
trees,
and are the binomial trees used in the binomial queues we
totally ignored when we studied heaps. Ya never know, eh?
Implementation trick: computing the size of a tree is a horrible
thought, since the pointers go the wrong way. So instead, let the
contents of a root node be -treesize, and update it while unioning.
Then M unions can be done in O(M) average time for most models of 'average'.
In union by height keep track of heights and union by making
a shallow tree the subtree of a deeper tree. Trivial mod.
Speeding up Find with Path Compression
So far, have linear average time but fairly easy to realize the
worst-case O(MlogN) time (enqueue the sets, then dequeue 2 and
enqueue their union).
Hard to improve union algorithm, since ties broken arbitrarily, so
need a faster find.
Path compression is a cute operation done during a find and
does not depend on the union algorithm. In path compression, every
node found on the path from node x to the root is simply made to point to the
root directly. On a find(14) the worst-case tree for 16 unions becomes
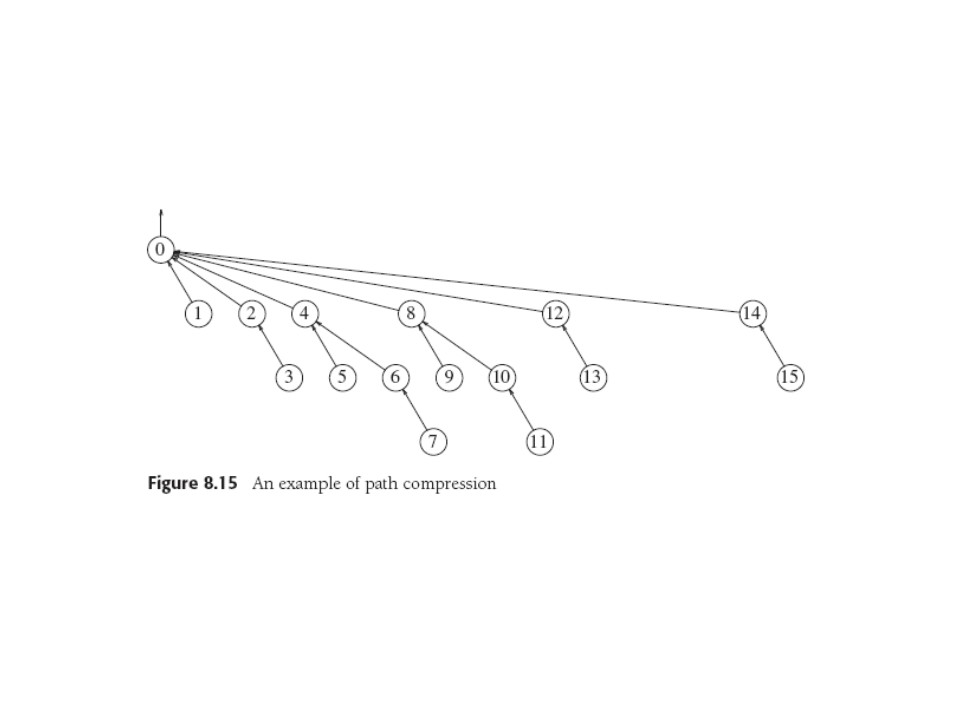
Again, a simple implementation compatible with union-by-size, but not
exactly with union-by-height, since it changes the heights. Fix is to
ignore that minor detail and re-interpret the (old) heights as "rank",
so we get union-by-rank, which is just as efficient.
Path compression does significantly reduce worst-case running time.
Worst Case for Union-by-Rank with Path Compression
Slowly-growing functions:
Recall or invent the recurrence for the time of binary search:
T(N) = 0, n ≤ 1
= T( ⌊ f(N) ⌋ ) +1, n > 1
For binary search, f(N) = N/2. Here T(N) is the number of times starting at N that we must
iteratively apply f(N) until we reach 1 (or less). f(N) is a
nicely-defined function that reduces N. Call the solution to this
equation f*(N).
Now in binary search, f = N/2: we halve N at every search step. As we
know,
we can do this log(N) times before getting to 1, so f*(N) here is logN
(much less than N).
Here is a table for f*(N) for various f(N). For disjoint set
algorithm analysis we're interested in f(N) = logN, and the solution's
name is log*(N), which we will see in several algorithm analysis
solutions (this lecture and later life).

log*(N) is just the number of times you have to re-apply log(N) to get
down to 1. So
log*(2) = 1, log*(4) = 2, log*(16) = 3 (now growing
slower than log),
log*(65536) = 4, and log*(2^65536) = 5.
So for
the real world, log*(N) <5 . As you see, log**(N) is the
number of times you have to apply log*(N), etc, so these log****(N)
functions grow very slowly.
Time Complexity of Union Find
If we do union-find with union by rank and path compression,
Theorem: If M operations, either Union or Find, are applied to N
elements,
the total run time is O(M log* N).
There is a rather straightforward
Proof in Wikipedia that makes Weiss's treatment
(Weiss 8.6.2, .3, .4)
look a bit
overwrought.
People also prove the average expected time is linear in M+N, under
various assumptions, such as that each tree in the representation is
equally likely to participate in the next union operation. Google
'time complexity union find'.
A Fast-growing Function
For fun: a fast-growing function. Its inverse is slowly-growing and
appears in some proofs of union-find complexity.
It was invented by Wihelm Ackermann, a student of Hilbert who was
looking for recursive (Turing-computable) functions that are not
primitive recursive (like exponentiation,
super-exponentiation, or factorial).
There are lots of "Ackermann" functions, one of
the most familiar being the Ackermann-Pe'ter function.
defined for nonnegative integers m and n:
A(m,n) = n+1, m = 0;
= A(m-1,1), m > 0 and n = 0
= A(m-1, A(m, n-1)), m > 0 and n > 0.
A(4,2) is an integer of 19,729 decimal digits.
That's A(4,2) = 2^2^2^2^2 -3,
A(4,4) = 2^2^2^2^2^2^2 -3,
A(4,n) = [n+3 2's] -3
There are larger numbers, too. Check out
Wikipedia, which has some nice "traces" of evaluation that show
how the function grows so quickly.
Summary
Yes, well... the analysis is too much for us now, PURELY
for time reasons. It goes on, it uses fairly complex reasoning,
and it winds up using log*(N).
You may want to remember from this one topic:
- slowly growing functions
- fast growing functions
- analysis of simple algorithms isn't necessarily simple.
Maze-Building Application
Weiss 8.7
This might be useful in your future. Nice application using
connectivity as the equivalence relation. Start with totally walled
up bunch of cells, knock down walls to outside for entrance and exit
cells: then pick
a wall at random and remove it if the cells it separates are not
already connected. After that removing more walls increases
connectivity and confusion.
Timing analysis: union-find dominates time, and number of finds is
number of cells (remove one wall per cell: there are N-1 removed
walls for N cells), and about twice as many walls as cells to start.
Somewhere between 2N and 4N finds per run, and so if we do union/find
operation in O(Nlog*N), it's quick.
Last update: 7.24.13








