Max Flow, Min Cut
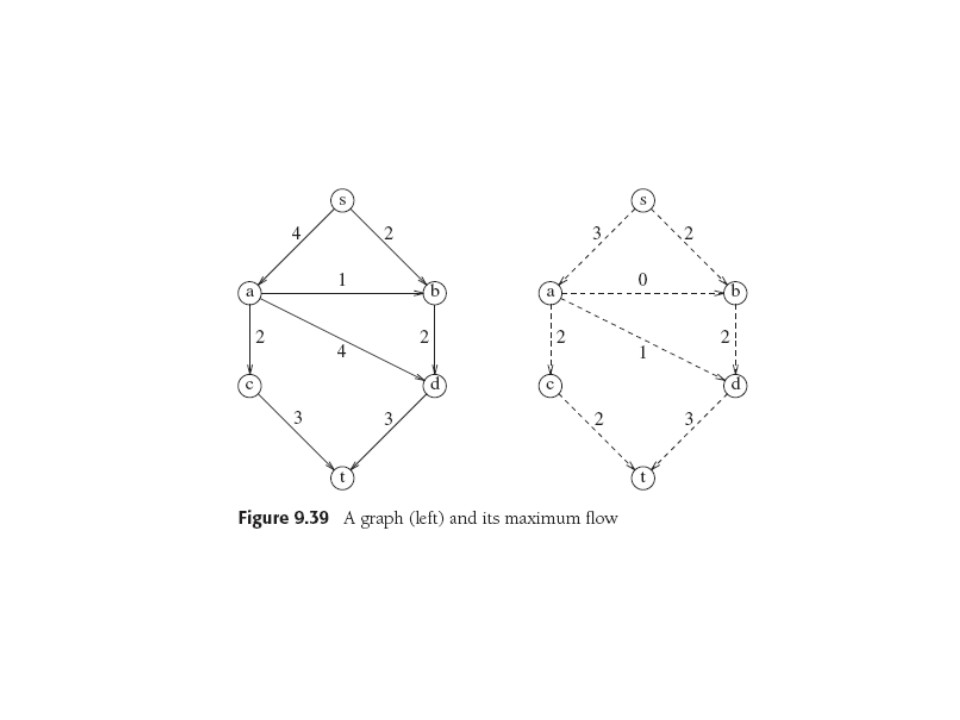
Max flow of lhs graph is 5, realized by the flow graph on rhs.
 Can we get flow = 6? The minimum cut value 5 shows immediately
why not. It looks reasonable, and indeed it's true, that Max Flow =
Min Cut.
Can we get flow = 6? The minimum cut value 5 shows immediately
why not. It looks reasonable, and indeed it's true, that Max Flow =
Min Cut.

Weiss Ch. 9.4
Water, oil, gas pipelines; bits across networks, electrical distribution, etc.
Model as graph (V,E) with capacities (not costs) on edges. Two special nodes s (source) and t (sink). At any vertice but s and t, flow in = flow out.
How much can flow between s and t?

Max flow of lhs graph is 5, realized by the flow graph on rhs.
 Can we get flow = 6? The minimum cut value 5 shows immediately
why not. It looks reasonable, and indeed it's true, that Max Flow =
Min Cut.
Can we get flow = 6? The minimum cut value 5 shows immediately
why not. It looks reasonable, and indeed it's true, that Max Flow =
Min Cut.
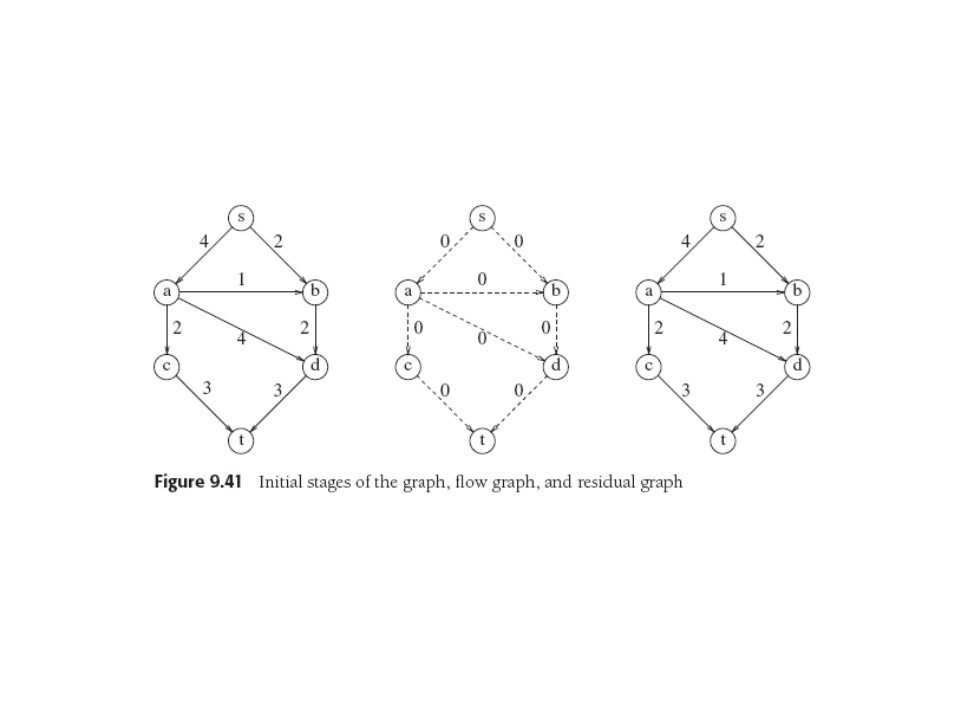
Proceed in stages: start with G and construct a flow graph
Gf
, which will change (we hope to increase total flow from
s to t). Initially
Gf has no flow anywhere.
We also need Gr, the "residual graph", which tells how
much flow can be added to each edge (= edge capacity - current flow);
so
initially this graph looks like G.
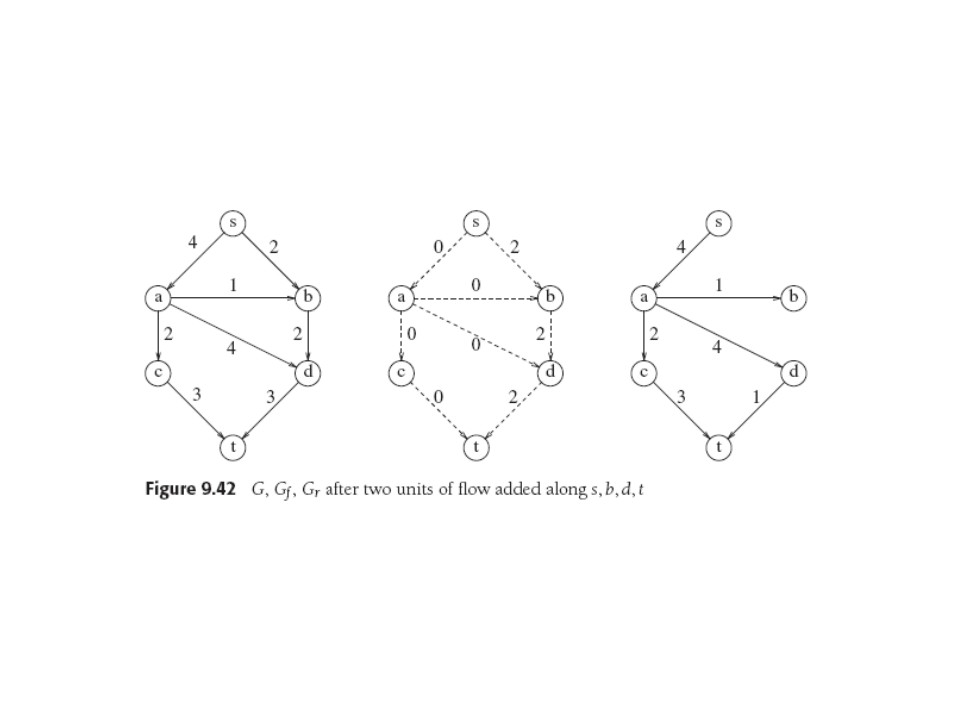
At each stage, find an "augmenting path" in Gr from s to t. Its minimum flow can be added to every edge on the corresponding path in Gf, after which we must recompute (by subtracting that path from) Gr . Stop when can find no paths in Gr. So it's a "nondeterministic" algorithm: we often have a choice of what path to use. Below, we choose s,b,d,t and send 2 units thru each edge. Edges used up to capacity in Gf are "saturated", and we remove them from Gr for neatness. So we get:
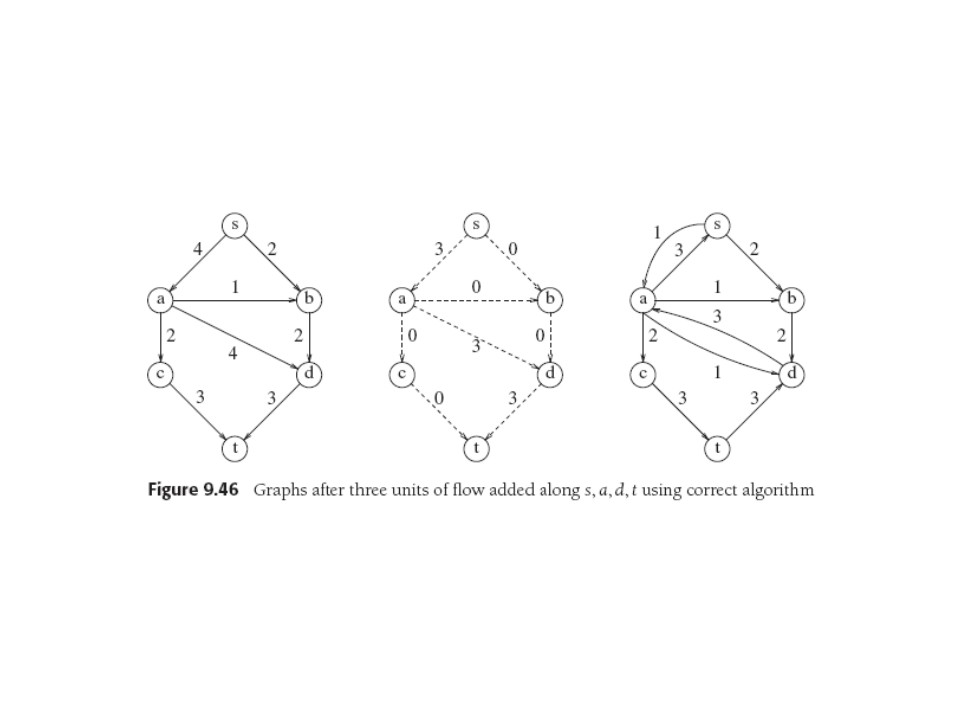
We can continue selecting paths and we might or not terminate with the max flow. In fact, choosing s,a,d,t (3 units of flow) initially leaves only 1 choice of path from s to t, and it only carries one unit, so we're stuck with suboptimal sol'n.
We need to allow algorithm to overcome suboptimal choices of path, or
to change its mind. Trick: whenever we add flow to an edge in the flow
graph, we add its reverse edge to the residual graph, representing
flow that we might want to go the other way at a later stage.
Below is G, the (seemingly bad) choice of s,a,d,t in
Gf, and in Gr both the original residual
(forward) flow
after putting it in Gf
and the
(slipsies, mulligan,...) flow opposite to what we just put into
Gf (those upward-pointing 3's).
So from here the algorithm can choose a new augmenting path, pushing some
flow backwards, e.g. s,b,d,a,c,t. This takes 2 units from edge a,d. Dass
it, no more paths, termination, AND termination implies max flow.
Termination
implies no path s,...,t in
Gr, so cut it with vertices reachable from s on one side,
unreachable on the other.
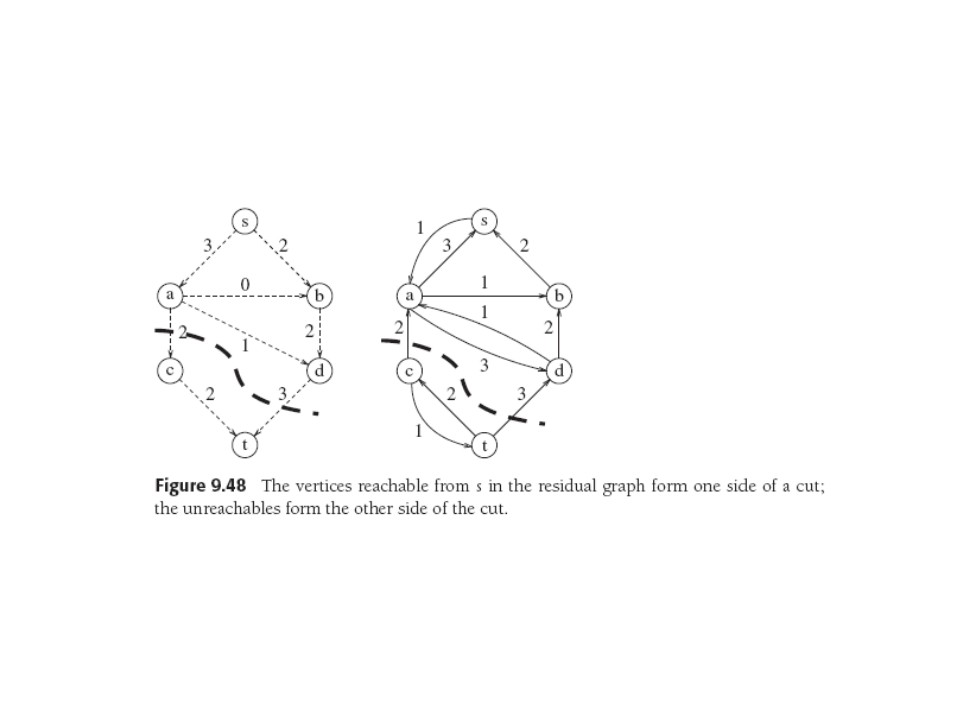
Original graph edges that cause the cut must be saturated else there'd be residual flow on one of the edges, implying an edge crossing cut in wrong direction. So flow = capacity of cut.
Analysis: terminates with integer flows, since flow increases by at least 1 at every stage. So with maximum flow f, get O(f|E|) (finding augmenting path by unweighted SP algorithm in O(|E|). Classic example on p. 392 shows why this is bad: one can waste too much time augmenting with skinny little edges and ignoring big fat edges. Choosing the augmenting path causing the largest increase in flow is almost like Dijkstra.
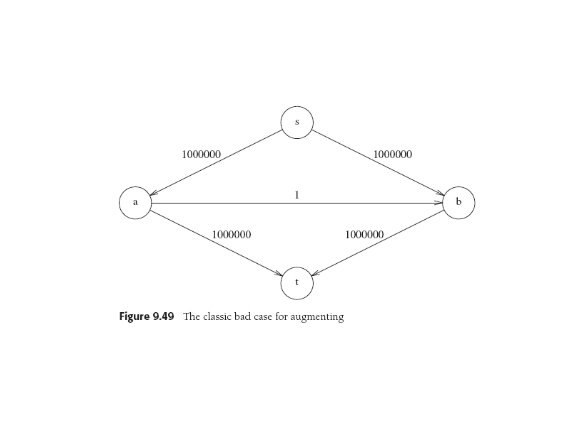
That gives O(|E|log capmax) augmentations to find the max flow, with capmax the max edge capacity.
Thus with O(|E| log |V|) to calculate each augmenting path, get
O(|E|2log|V|capmax), and if capacities are small
integers, = O(|E|2log|V|).
More tweaking and ideas (choose augmenting path with smallest number of edges)...pp 392-393. Improved bounds, faster special (but common) cases, etc. Min cost flow a research problem (unit of flow has a cost, what's cheapest max flow routing?).