
Minimum Spanning Tree
Weiss Ch. 9.5
MST of UNdirected graph is usual case: tree that connects all vertices
of G with minimal cost. So G must be connected. MST not necessarily
unique.
Natural idea: how connect all nodes cheapest?
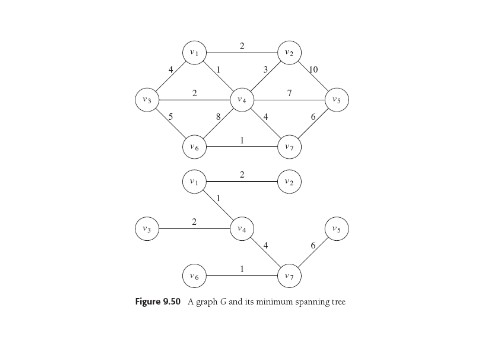
Elementary reasoning assures us a greedy approach should work.
Prim
Pick a root and then add one vertex at a time. Just add that vertex v
and edge from u to v, such that u is in the tree, v is not, and
Cost(u,v)
is minimal amongst all such edges.
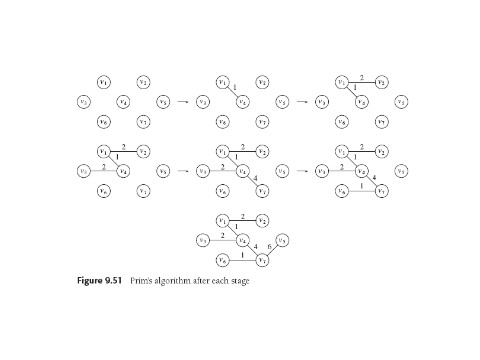
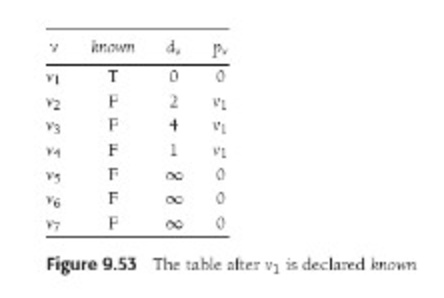
This is just like Dijkstra's A, only dv is the cost of one
edge, and the update rule is simpler. Thus Weiss brings back his
tables, which for instance look like this: Here we have just chosen
v1 as root, and its three naighbors v2, v3, v4 have their edge costs
inserted.
They're not in the tree yet so they're unknown, but it's easy to see
we're going to pick v4 to add next, and when we do the cost of adding
v3 is going to drop to 2, and v3's pv will change from v1 to v4.
So as for D's A, order O(|V|2) without priority queues
(heaps), optimal for dense graphs and with binary heaps get
O(|E| log|V|), good for sparse graphs.
Kruskal
Another greedy plan: select edges in order of of smallest weight,
accept one if it doesn't cause a cycle.
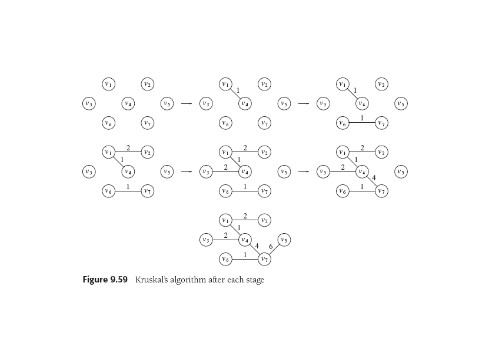
K's A starts with a forest of single nodes, which are merged to form
one final MS tree. The underlying algorithm is union-find, but we're
going to want a priority queue too. We define
nodes to be
in the same set if they are connected in the current spanning forest.
Rather than sort the edges, heapify and deleteMin. Then if both ends
(u,v) of an edge are in same set, reject it (cycle). Else union the
two sets containing u and v. Worst case you have to examine all the
edges
(there may be one really big one); O(|E| log |E|), dominated by the heap.
Depth-First Graph Search
Not only a key AI technique but useful for computing several graph
properties and problems. DFS just visits every node, then its
successors, recursively. With trees this is super-simple, with graphs
one needs not to get stuck in cycles so it's only simple. Weiss has
4-liner basic program, p. 400.
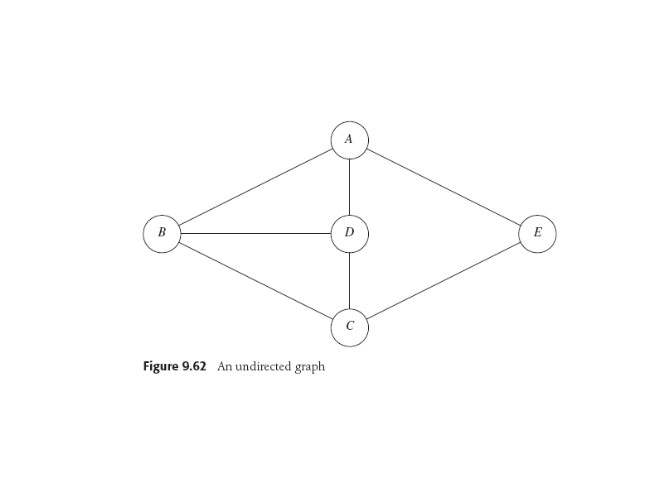
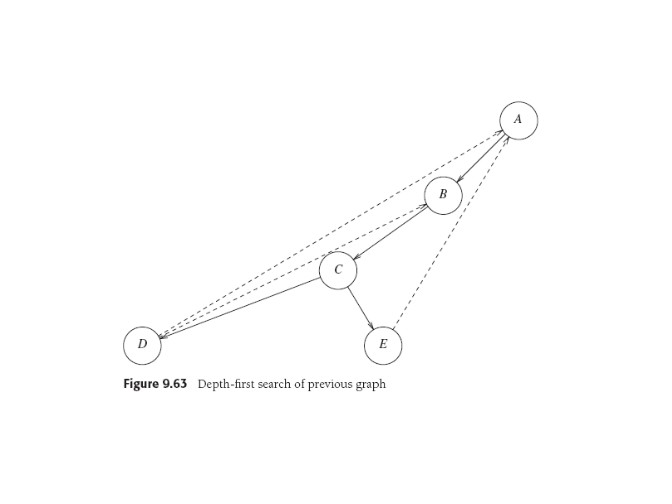
DFS Visualization
DFS induces a "depth-first spanning tree" on the graph, since it
doesn't cycle. In AI we often talk of a search tree in a state-space
graph. To relate the two one can use "back edges" that are not taken
in the search, which we can imagine being generated at each newly-visited
node: all its successors that have been visited already are given
back edges pointing at them. An unconnected tree needs a re-start for
the search process if all nodes aren't visited when the DFS ends.
Establishing Properties etc. with DFS
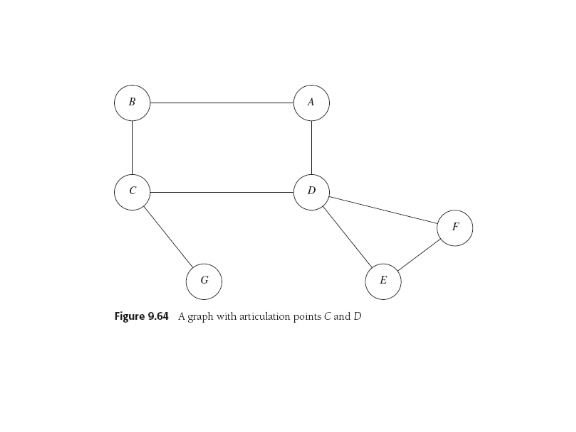
Biconnectivity: A graph is biconnected when it cannot be
disconnected by removal of any single vertex. Clear logistical
analogs--e.g. redundant routes, components. Disconnecting vertices are "articulation points".
Weiss gives pseudocode and discusses some proofs and niddles.
DFS is the basis of a linear-time algorithm to find articulation points,
thus answer the biconnectivity question.
- Do DFS, make DFS tree with backedges, number vertices Num(v)
in order of
visit.
- For each vertex v compute the lowest-numbered vertex Low(v) that
can be reached from v by 0 or more tree edges and possibly a backedge
(in that order)
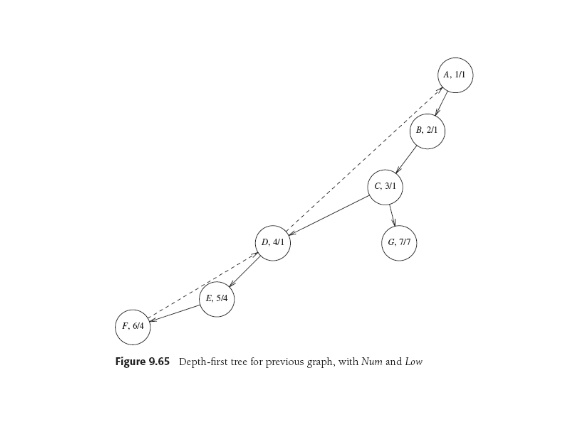
-
Low(v) can be efficiently computed from its definition: Low(v) is the
minimum of:
- Num(v) if no edges are taken
- the lowest Num(v) amongst all back edges (v,w) if take no tree
edges, one back edge.
- The lowest Low(w) amongst all tree edges (v,w), a recursive defn
that moves down the tree.
Biconnectivity...
Since we need to compute Low(v) for all v's children before computing
v's,
we have postorder traversal algorithm.
If Num(v)>Num(w) it's a tree edge, else a backedge. So to compute Low(v),
use adjacency list to look at all nodes adjacent to v (from adj list),
keep track of minimum. That's O(|E|+|V|).
Articulation points?
- root is articulation pt iffi it's got >1 child.
- v is a.p. iffi v has a child w s.t.
Low(w) ≥ Num(v).
Why?
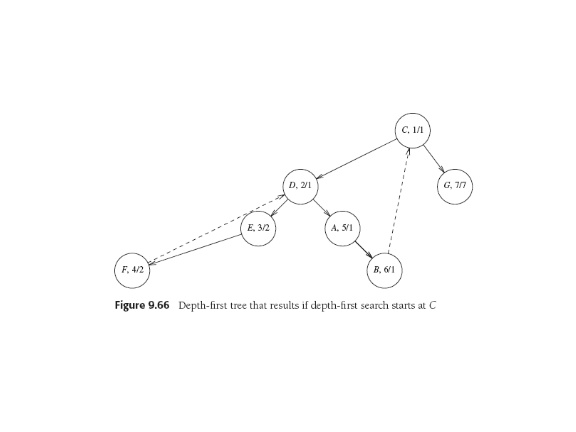
Defns say C and D are articulation points. D's child E only has one
way to get to any node above D: go through D.
Naively implementing all this takes three passes, preorder traversal to get
Num(v),
postorder to get Low(v), Third pass finds articulation points. BUT!
job can be done much more elegantly (Code in Figs 9.67 - 9.69).
Euler Circuits and their Ilk:
These puzzles were the subject of the first work in graph theory in 1736.
Puzzle: Draw these figures w/o lifting pencil, each line covered
exactly once. And can you finish where you started?
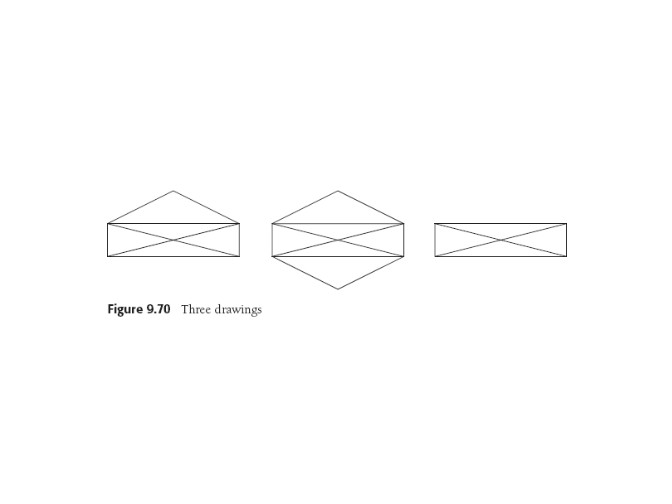
"Euler path (tour) and circuit"
problems: traverse all the edges (NOT vertices!!) just once.
The Euler circuit ends where it started,
Form of solution is same as path, so Weiss does circuit. Some things
obvious:
- circuit only possible with connected graph, all vertices of even
degree.
- If two (exactly) vertices have odd degree, can tour by starting at
one and ending at other.
- more than two odd-degree vertices, no tour.
Algorithm builds up sub-solutions by splicing. This graph has an Euler circuit.
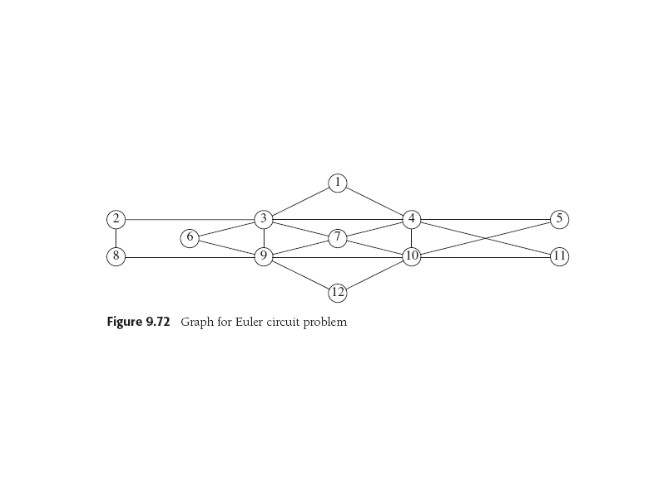
If start at 5, a DFS might find 5,4,10,5, so we'd have a sub-circuit
and a remaining problem:
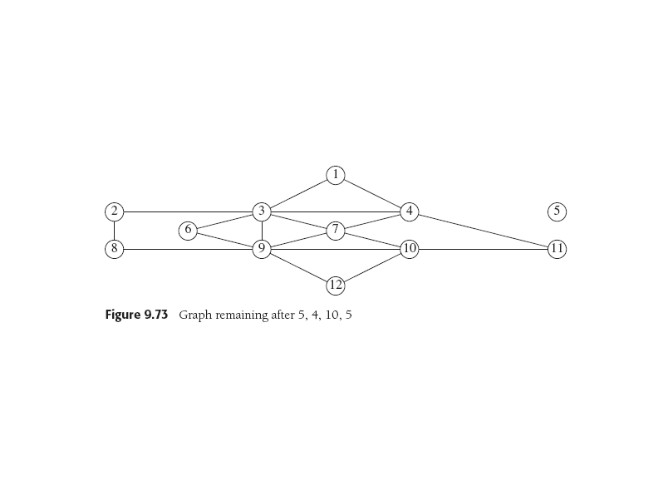
If then start at 4 could DFS and get 4,1,3,7,4,11,10,7,9,3,4. Splicing:
5,4,1,3,7,4,11,10,7,9,3,4,10,5. Etc.
Splicing is O(1) if path is a linked list. Maintain pointer to last
edge scanned in adj. list so can start there later. Begin next
depth-first search at start of the splice point...so work in vertex
search is O(E) over the algorithm, so can make whole job O(|V|+|E|).
Finally:
Hamiltonian cycle is simple cycle in an undirected graph that
visits every vertex. Strangely, no efficient algorithm for it is
known.
You could get famous if....
Directed Graphs:
DFS can be extended to directed graphs and used to find "strong
components",
which are subsets of strongly-connected vertices (a path between any
two).
Directed Graphs
Recall a graph is strongly connected if there is a path from
every vertex to every other vertex.
Can DFS a directed graph but from any given vertex may not visit all
nodes unless graph is strongly connected. So restart search
elsewhere. Process gives forward and backward edges but also
cross edges.
A digraph is acyclic iffi it has no back edges.
DFS can test strong-connectedness and find strongly-connected
components. Doing it with two DFS's is easier than with one,
(W. 9.65).
Last update: 7.24.13












