
Workshops, Labs, Tutors
Scheduling:
No workshops or labs in first week.
Workshop TAs will organize a poll for Workshop times.
Lab reports are graded (see grading info from main page), WS has
participation points (5% of course total points). And there are
WS quizzes in class, maybe extra Success Facilitation Surveys too.
It's not about grades, of course... they are a side-effect.
Workshop times and places will be made up an announced soon.
Tutoring:
Computer Science Undergraduate
Council offers 2-6 hours of FREE tutoring, every day M-F, in Hylan
301. It
will be an informal setting where you can arrive at any time and ask your nagging
questions about CSC 171, 172, and a combination of other introductory and core
computer science classes.
The schedule can be found here: CS
Tutoring Schedule.
In 2014, Hassler Thurston (jthurst3@u.rochester.edu) is the president
and a good point of contact.

172 Goals
- Maturity and practice translating "word problems" to programs.
How to get started and carry on formalizing and solving a
computational problem.
- Maybe extend Java skills, introduction to C, hat-tip to Scheme
(generally useful + CS173).
- Eclipse envt. seems a super idea.
- Why Java? Intro claims it's "better than C++". Agreeed, but why any
real language? Maybe to banish all ambiguity.
- Basic data structures: vocabulary, use, raison d'etre.
- Basic algorithm analysis.
- Develop both individual- and team- work skills.
General Advice
- Come to class.
- Be Polite: takes some sacrifice (see above), good exercise in
diplomacy.
- Buy and read the textbook, course materials.
- Do the work.
- Confront your fears: seek out the uncomfortable. Then either
deal with it or work around it as you like (e.g. Generics!).
- Don't get depressed -- See advisor, prof, somebody and talk.
- Always strive for a liberal education (cf. 172 Resources).
Your Enemies
- Horrific peer examples, Dysfunctional and Decadent culture,
Distractions, Media.
- Profs with low expectations or standards.
- Bad time management (esp. procrastintion).
- Bottoms-up or self-defeating thinking:
"I haven't had a course in X so it's unfair
to expect me to learn X, [because I can't]".
More efficient: top-down,
goal-directed learning.
- You're not making it up, you ARE overloaded! Prioritization and
Discipline are all I can suggest.
Your Advantages
- Native talent.
- Strong background (it says here...).
- Good students can do about 5 times what I consider possible.
- UR's Massive support infrastructure (e.g. deans, vice-deans,
writing center, LAS, tutors, TAs,
psyche svcs, me, other profs...)
- Data Structures as 'mature' CS displine...tons of good texts,
on-line tutorials, worked problems,etc. etc.
- Curiosity and Enthusiasm: Embrace and
enjoy learning new things. Learn how to learn. (Psst... that "course
in X" likely wouldn't have covered what you really need.)
Big Oh Intro
Question: How does computation time grow as input size grows to
infinity? The Order (O) expresses (an upper bound on)
that growth rate. For this lecture we take O to mean "rate" not "bound on rate"
Technology? Pfui!: faster computers make operations faster, but it
turns out that doesn't change the Order of a computation, which
dominates all constant speedups. It's a rate of growth.
E.g.s: The time to read or print a file grows linearly with file
size:
N times bigger, N times longer. The time to do long multiplication
grows as
the square of the number of digits:
XXX N
XXX N
-----------
XXX N*N multiplies
XXXX
XXX
----------
XXXXXX 2N output
So...?
Combining Orders: Intro
Say T1 and T2 are running times of two processes. If for input length N
T1(N) is O(f(N)) and
T2(N) is O(g(N))
⇒
T1(N)+T2(N) is O max(f(N) + g(N))
= O(f(N) + g(N))
So above, O(2N) for input, O(2N) for output,
O(N2) for calculations, so total time is
O(4N + N2) = O(N + N2) = O(N2).
A higher growth rate always dominates a lower: e.g.
x2 > Nx
when x > N.
Growth Plots
The intractability of high growth rates:
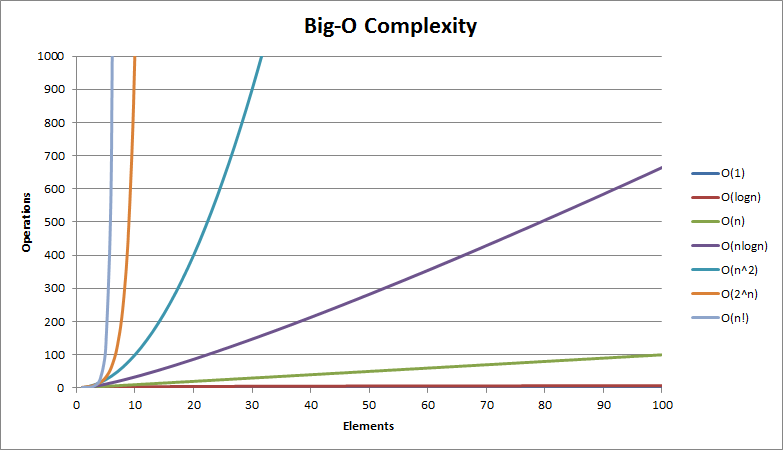
below, log-log plot

Enough: to be done right later.
Case Example: Duplicate Detection
The Problem: find identical items in a list. Practical!
E.g. presenting
search requests.
One solution: compare each item to all items earlier in the list.
Core of the computation is:
for (int i = 1 ; i < a.length ; i++){
for (int j = i - 1 ; j >= 0 ; j--){
if (a[i].equals(a[j])) found = true ;}}
Analysis?
Loop analysis. i counts up from 1 to length (that is N, the
problem size), and for every i, we have j
counting down from i-1 to zero. So...???
Answer: 1 + 2 + ... + N repetitions: sum = (N*(N+1))/2 =
O(n2).
Dup. Detection: Hashing Solution
Solution: for each list item, hash(item) = is
a simple O(1) function to give a repeatable, "randomized"
location in a big array.
Look at hashed location:
if location empty, put item there, unique (so far). O(1).
if item's there already, it's a match. O(1).
if a different item's there already, we see why
hashing's so interesting....
Analysis: not obvious, goes back to Knuth and beyond. Good news is
that
at the price of more storage, we get linear O(N) performance (each
comparison takes constant O(1) time.)
Live Demo
This
Worked
in
Rehearsal
...
Honest!
Runnable Code
Source Code and class
files
(run on unix-like KDE (java 1.7) , maybe not on linux's ubuntu (java
1.6). I had to fiddle to get it to work on a Mac...sigh.
>>java CBDupSearch 1000
simpleSeach
631 unique values
Comps == 499500
n(n-1)/2 == 499500
Total execution time (secs): 0.027
>>java CBHash 1000
632 unique values
Comps == 1368
Total execution time (secs): 0.0
Experimentation: O(n2) method
Sort of thing we do in projects... if you can generate date,
exploit it.
Output to disk, use excel or whatever to graph -- profs love it.

This plot's worth about a C -- no title, axis labels, or units.
End of Duplicate Search Example
Mathematical Background
Weiss's reviews (Ch. 1.2, 1.3) are cursory. If they're OK for
you,
quite a good sign.
But feel free to look
elsewhere. (All together: "Oh boy, I get to learn something new!").
- 172 readings links.
- 172 resources links.
- MTH 150 (text) --example of next item.
- Carlson Library, Amazon (keywords like "discrete mathematics for CS",
"basic mathematical techniques for CS")
- Wikipedia is usually quite good on math tutorials.
Weiss 1.2 -- Math Review
To-the-point 5 page section.
- Exponents: e.g
(xa)b = xab,
- Logarithms: Useful properties, all derivable from the definition.
A logarithm is an exponent:
(xa = b ) ⇔ logxb = a,
x > 0, b > 0, and b ≠ 1
Four Basic Properties
1. logb(xy) = logbx + logby
2. logb(x/y) = logbx - logby
3. logb(xn) = n logbx
4. logbx = logax / logab
1. is Weiss's Theorem 1.2 and is where the slide rule came
from -- why early calculators (like celestial navigators) loved
logs.
4. Is Weiss's Theorem 1.1:
logs of a number to different bases differ at most by
a constant multiple. Algorithmic Analysts love this --
the complexity we're here to formalize doesn't depend on the base. Notice
how all the proofs flow from the above simple definition.
More Properties
logb1 = 0
logbb = 1
logbb2 = 2
logbbx = x
blogbx = x
logab = 1/logba
alogbn = nlogba.
- Series: pretty basic. First equation easy to see by considering
the
binary representation of both sides. Geometric Series are important: sum
is over terms whose exponent gets larger linearly.
Note the ingenious and elegant proof technique that subtracts a
multiple of a series from the series itself and gets an enormous
simplification
(to 1, in fact!). Cute and useful In Later Life.
Big Oh and Geometric Series: We know that the order
O() of a sum is the order of the largest summand. Thus in
Decreasing Series the first term dominates and in
Increasing Series the last term dominates. Neat, eh?
Last, arithmetic series (sum is over terms involving an N not in
exponent that gets larger.) Weiss appeals to the famous problem of
summing numbers from 1 to N, ("everyone's first induction
proof" for some generalized solutions. He shows some other useful
series.
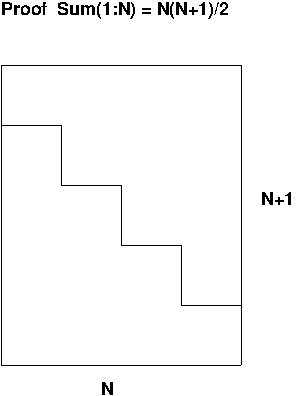
"We don't need no stinking induction!"
- Modular Arithmetic: Important for Crypto, less for us. Concept of
a prime is basic: The
theorems are an intuitive fact following from the definition of prime, then
conditions for multiplicative modular inverse to exist, then a pretty
and non-intuitive fact about
modular square roots. Ignore for now, remember it's here in case...
- Proofs:
Types of proofs: induction, counterexample, contradiction, cases and
construction (not mentioned). Induction is basic for Algorithm
Analysis. Make sure you get it.
- Recursion: Idea shouldn't be new to anyone -- everyone seen this?
Base case that stops recursion, recursive case that uses fn itself
in computation, as in:
Bases: fib(0) = 1, fib(1) = 1:
Recursion: fib(n) = fib(n-1)+fib(n-2)
Thus rather like inductive proof with known base case and inductive 'assume
it works' step.
Geometry and Proofs
On the One Hand
Equations are the boring part of mathematics. I attempt to see
things
in terms of geometry.
-- Stephen Hawking
On the Other...
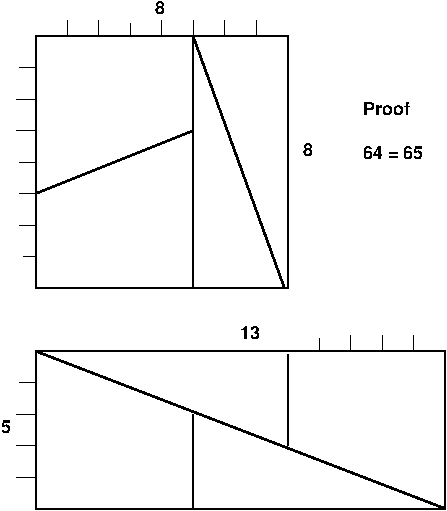
SFS
Convince me, however you like*, that
1 + 3 + 5 + 7 + ... +(2n+1) = (n+1)2
* Sometimes we say: "Prove" (but that may sound scary).
And is the graphical solution to sum of 1--N an inductive proof?

Last update: 6/25/13 CB







