
Stacks, Queues
Weiss Ch. 3.6 and 3.7
Stacks are a useful conceptual tool. Capture notion of being (maybe repeatedly)
interrupted, or redirectered, to a new problem (that may or may not
be related to the original). When the new problem is done, work on
original
is resumed, perhaps using results from earlier interruptions. "Last
in, First out!". Often modern processors have stack operations in
their instruction sets.
Queue is British for Line (as is "in line", which is American for what
we in NY know is "on line"). Some countries don't know the concept,
BTW.
It captures the natural idea of "first
come, first served". Queues are ubiquitous in service-oriented,
manufacturing, military, logistical, computational, financial,...
enterprises. Poisson (1781-1840) gives his name to the probability
distribution that results, as in atomic decay, telephone calls at an
exchange, web accesses, thruway tool booths, disk accesses, etc., from exponentially
distrbuted interarrival times for requests. So there are formal ways
into the discipline that allow analysis and design of real hardware
and software systems.
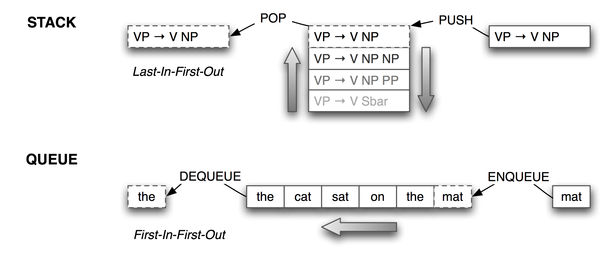
Stack ADT
Traditionally we think of those plate-dispensing stainless steel carts
at a cafeteria, with a stack of plates resting in a hole, riding on a spring so
only
the topmost is visible and accessible. The basic things to do with a
stack are to take (remove) the top item (pop), put a new item on top
(push).
I guess since stacks can be implemented with arrays, and trying to
pop
an empty array-stack could result in an index-out-of-bounds error,
trying
to pop an empty stack is usually considered a logical error. Given that,
we need an isempty test for stacks, and for
efficiency we often see something like peek or top to get the value
of the top item without removing it.
These are all O(1) operations.
Stack Implementations
Arrays and lists are both natural. With list you push and pop by
adding
a new, or removing and returning, the first item.
Array is clear: stack ADT has a data array and a top-of-stack index (-1 to
start), which are changed in the obvious ways. Stack grows from start
of array toward its end; overflow is an implementation error but not a
logical one: logically stacks are infinite.
Stack Applications
Operating Systems: interrupt stacks. Parsing: table-driven
context-free parsers. Programming languages: method (subroutine,
function) calls via activation records or
stack frames. Non-standard use (grabbing from middle of stack, say)
yields "teleportations" or continuations (Scheme).
Arithmetic-oriented operations: infix to postfix conversion,
postfix evaluation.
Warm up: balancing symbols like parentheses, brackets, comment
delineators... (W. p. 84). To balance ()[]{} chars, say:
e.g. {([]}), [ errors. {()[]} OK
Create new empty stack, read file by chars.
If char is one of ([{, push it
If char is one of )]}, pop stack. If result not the corresponding opening
symbol, error. At EOF, if stack not empty, error. else OK.
For below, also see the Stack and Arith. Expressions PPTs in the syllabus for this
date.
Infix with precedence: so 1+2*3 means 1 + (2*3). Other issues like
what
1-2-3 means...evaluation order. Reverse Polish notation, or Polish
postfix, or postfix, is unambiguous w/o parentheses:
1+2*3 goes to 123*+.
Evaluate (Easy!): work L to R: if see a number, push on stack. If see
operator, pop however many arguments it needs off the stack, do it,
and push result on stack. (W. p. 85-87).
Not quite so neat, but still simply doable with a
stack, is conversion from infix to postfix. (W. p. 87-90).
Queue ADT
Basic: enqueue (join the end of the line) dequeue
(move off the front of the line). Presumably peeking at the front
value and testing emptiness could be in a package as well. All O(1) operations.
So ADT represents the data items and has values for front and back,
currentSize, etc.
Queue Implementations
Again, lists (obvious) and arrays. Unlike a stack, both ends of a
queue move, so with an array implementation need to keep "front" and
"back" indices, which move as en-and-de-queuing happen: of course
enqueuing also updates an array element.
The array length must be at
least as large as the desired maximum queue size unless something cute
goes on behind the scenes. The array is made "circular" using
mod() or % or just a test to set back or front to the start of the
array if they move off the back.
The empty queue has the back pointer
"up ahead" of the front. Enqueueing the first item makes it
at the front and back both, and more items push the
back of the queue farther away from front.
Queue Applications
Super-common, help create fast solutions (later in Graph theory
algorithms).
W p. 95 goes thru an impressive list of practical real-life
applictions, including commerce, communications, computer components
and networks. Queues are used in physical simulations (e.g. games),
and to simulate and thus get results on systems that are not
analytically solvable by queueing theory.
Even simple systems involving queues
can be unsolvable, despite tools going back to
Poisson and powerful later methods like the Laplace-Stieltjes
transform.

Last inspection: 5/27/14


