
AVL, Splay, B-Trees (Java Sets, Maps)
Weiss Ch. 4.4-4.8
Definitions
AVL tree is a BST with a balance condition: height of every
node's left and
right subtrees may differ at most by one. At most, an AVL tree's
height is 1.44log(N+2)-1.328 (see below), usually a little bigger than
log(N).
The minimum number of nodes in an AVL tree of height is the
Fibonacci-like
S(h) = S(h-1)+S(h-2)+1, S(0) = 1, S(1) = 2, yields above bound.
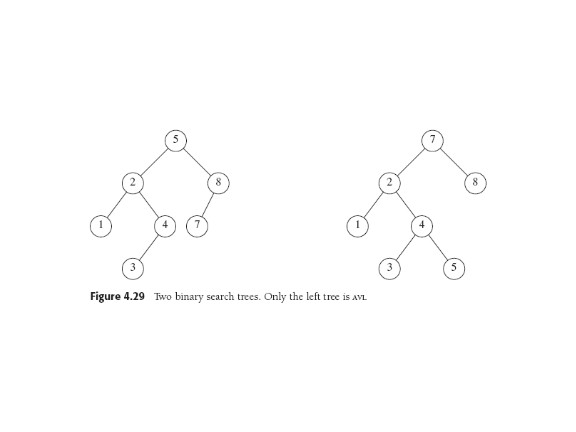
Keeping your Balance
Four cases needed to keep the tree balanced on insertion;
two symmetrical versions of two basic cases. The necessary operations are called
(single and double) rotations and have an intuitive interpretation using a tree diagram.
(W p. 125-132.)
R
N M
L1 R1 L2 R2 subtrees
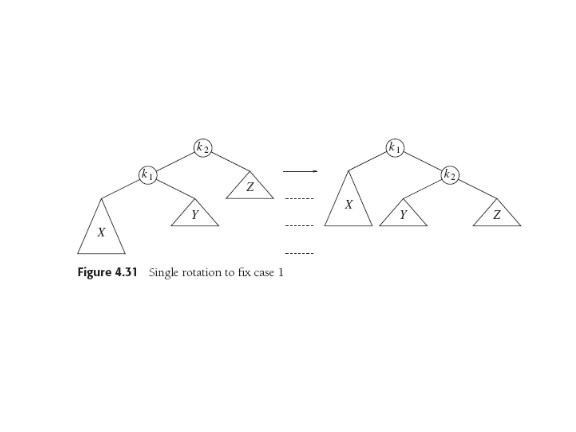
Single rotations come from Case 1 (inserting into L1): Case 4 --
inserting into R2-- is a mirror
image case.
Cases 2 and 3 cover insertion into R1 or L2.
SINGLE ROTATION
DOUBLE ROTATION
oops...
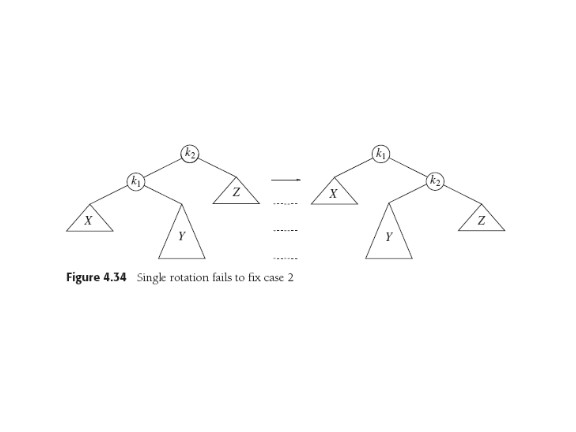
aha! But note Figs 4.35, .36 badly drawn IMO... horiz. dashes don't
corresp. to levels, and trees B, C should be deeper.
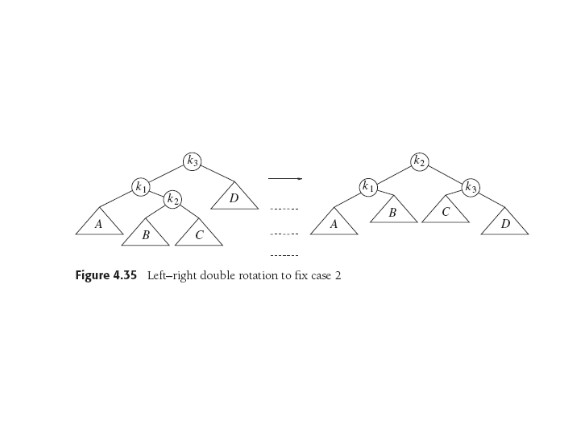
Good examples pp 129--132.
Last Words
Should convince selves that rotations
1. preserve BST property
2. preserve AVL property
Managing AVL trees requires bookkeeping information such as the {-1,
0, 1} subtree balance factor, or explicit node heights (as in Weiss).
Deletion in AVL trees is a bit complex and can take more than logN
time. Fairly simple mod of BST deletion, involving rebalancing.
If deletion is rare, easiest is "lazy deletion": leave node in place
but
mark it "deleted".
As usual, Weiss provides class defs, code for insertion, rotations,
height computation,
and tree balancing, along with informative commentary, pp 132-136.
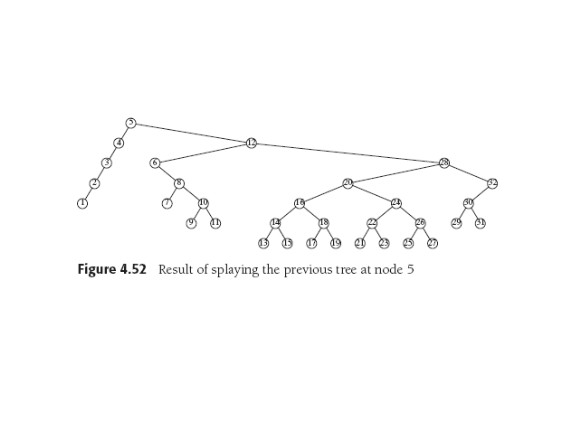
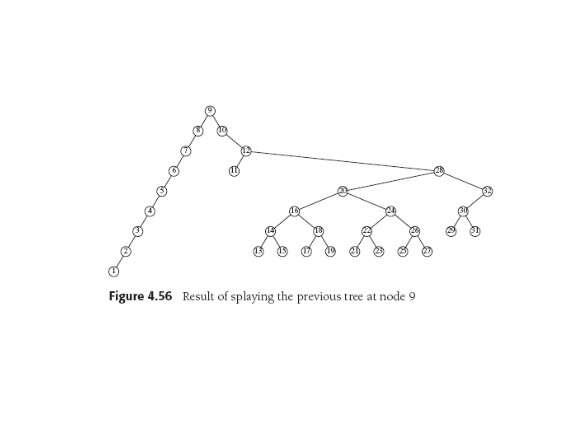
Splay Trees
W. 4.5.
Idea is to adjust the tree, generally after every
operation, so that that operation would have run faster. Motivated by
the
abstract idea of good "amortized" time: inefficiences are not
repeated, so the average performance is good. Also the practical
observation that if we just requested element E there's a very good
chance of our requesting it again, soon. So in a splay tree,
when a node is accessed it is moved to the head of the tree, and along
the way, the tree is partially rebalanced all the way up to the top.
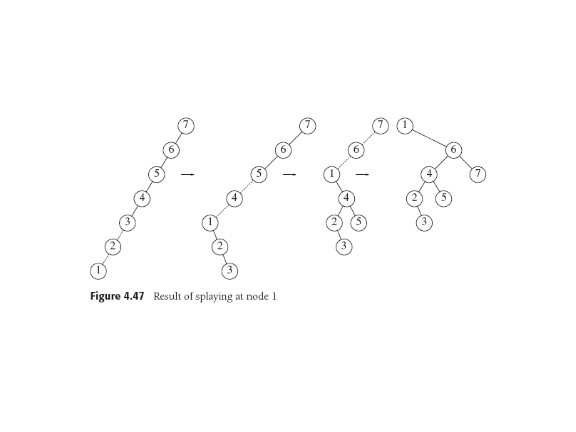
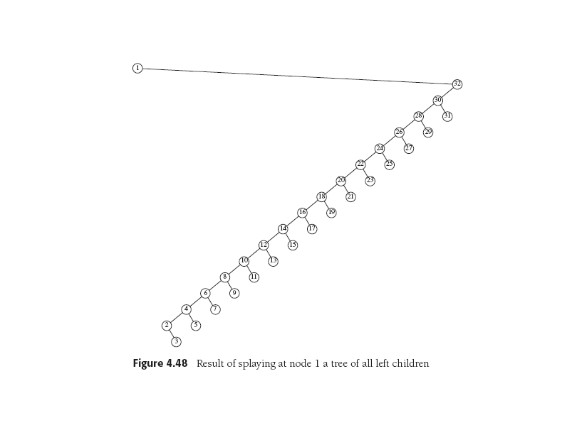
We can move a deep element to the top by single rotations, but that
turns out to push other nodes deeper. In the worst case, insert 1...N
in order to get all left sons, then search for 1 (time N); then 2
(time N-1),...and finally when all finished, "tree" is back where it
started (!) and of course time is Ω(N2).
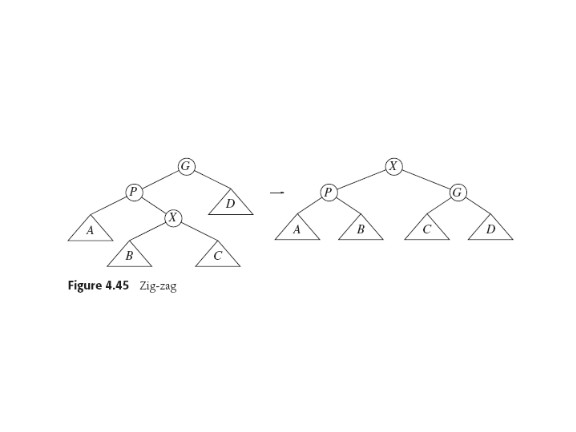
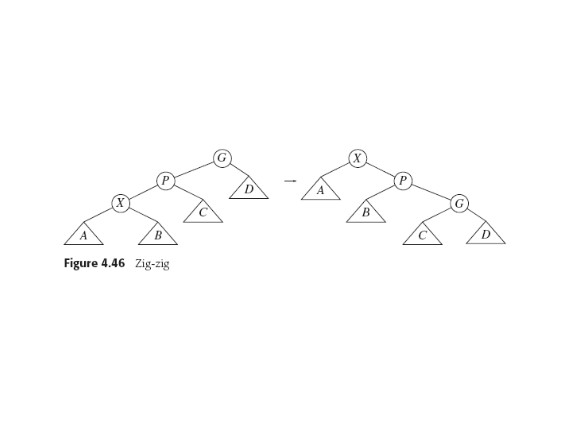
Hence splaying, which
is modified version of that idea, with a couple of cases (zig-zag
and zig-zig), that
determine what sort of rotations to do to whom.
Why Splay
- Good (NlogN) amortized performance
- Promotes most recently accessed item to top
- Also roughly halves depths of most nodes on access path
- But.. some shallow nodes can be pushed down 1 or 2 levels.
- Easy algorithms, few cases, no height or balance bookkeeping.
- But... hard to analyze!
- Lots of improvements possible: Ch. 12
AVL Animations
Lots of these are interactive and so rather boring, since lots of
typing's involved.
JHU demo.
Perhaps this
AVL Tree Demo is better.
Red Black Trees
Weiss 12.2.
Red Black Trees are binary search trees. One set of conditions:
- A node is either red or black.
- The root is black.
- A red node has black children.
- Every simple path from a given node to a null reference
contains the same number of black nodes.
All this implies that the longest path from root to leaf is no more
than twice as long as the shortest path ditto. And that the height of
a red-black tree is at most 2log(N+1).
Red-black trees are used in Java and generally may be more practical
and popular than AVL trees.

Thanks, Wikipedia.
Threaded Binary Tree
The astute reader will have noticed that there are unused pointers in
a BST. Quel Horreur! Terrible waste, tsk, tsk.
A binary tree is threaded by making all right child
pointers that would normally be null point to the inorder successor of
the node, and all left child pointers that would normally be null
point to the inorder predecessor of the node.
-- Chris Van Wyk, Data Structures and C Programs, Addison-Wesley 1988.
Note we do need a little "bit" of overhead that says whether a pointer
is to a child or is a thread. Else infinite recursive loops beckon.
A threaded binary tree makes it possible to traverse (in-order) the
binary tree with a linear algorithm that avoids recursive calls.
It is also possible to discover the parent of a
node from a threaded binary tree, without explicit use of parent
pointers or a stack, albeit slowly. This can be useful where stack
space is limited, or where a stack of parent pointers is unavailable
(for finding the parent pointer via DFS).
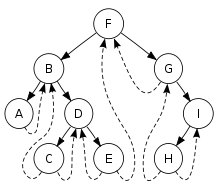 (from Wikipedia)
(from Wikipedia)
Traversals Redux
Claim: Inorder traversal can print out all items in BST in sorted
order in O(N) time. Why (twice)?
Height of node is max of heights of L, R subtrees +1. Hence postorder
traversal needed to compute it.
Label each node with its depth? root is 0, then recursively add 1 to
root of each subtree. Preorder!
To program these, handle null case first, only need to pass in pointer
to root of (sub) trees, no extra variables needed.
Level-order traversal (Breadth First Search, for example) -- visit a
node
and enqueue its children, repeat until done.
B-Trees
These are for massive amounts of data stored on disk. Their nodes are
related to the size of disk blocks. Weiss gives devastatingly
convincing justification for why once disks are involved the "time
complexity" rules have to change. 7200 rpm, means 1/120 second or 8.3
ms/rev. So disk accesses are about 9 or 10 ms. So billions of
instructions = 120 disk accesses. For 10M-long database, get
log of 10M accesses, or around 25, or 5 seconds per query.
Solution: shallower trees, and that means k-ary, not binary.
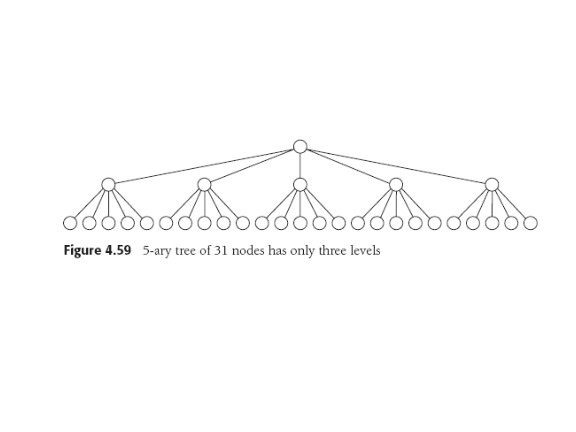
B-trees are M-ary search trees with, therefore, more complicated
keys. All internal nodes are actually key nodes: data is only stored
at the leaves.
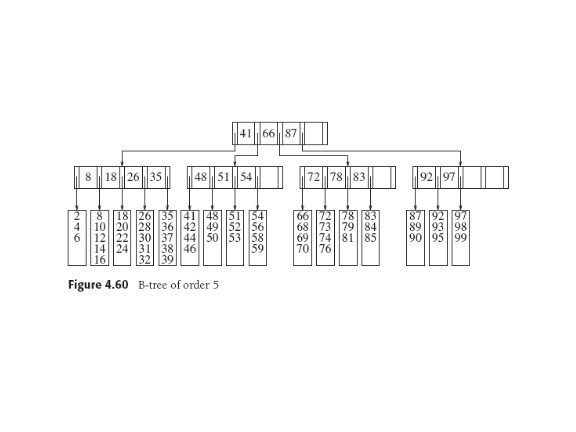
- Data stored at leaves
- nonleaf nodes store up to M-1 keys to guide searching; key i
represents smallest key in subtree i+1.
- root is either leaf or has between 2 and M children
- All nonleaf nodes have between ⌈M/2⌉ and M children
- All leaves are at same depth, have between ⌈L/2⌉ and
L data items for some L.
- M and L chosen depending on disk block size.
Designing a B tree means fitting its nodes into disk blocks. The two
main variables are M, the number of keys accomodated in internal
nodes
(hence M-ary tree), and L (number of items in a leaf).
Insertions and deletions call for pretty obvious splitting and merging
operations, and sometimes swapping data between nodes.

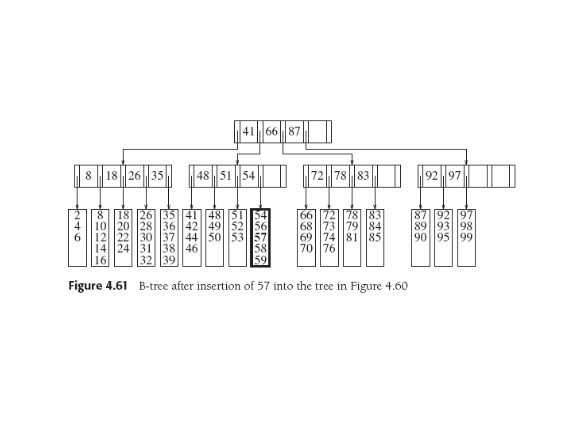
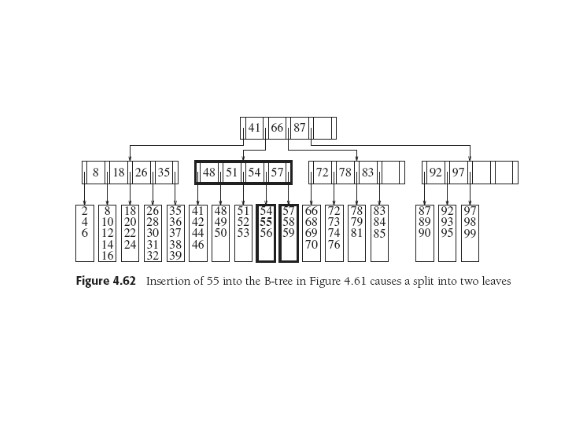
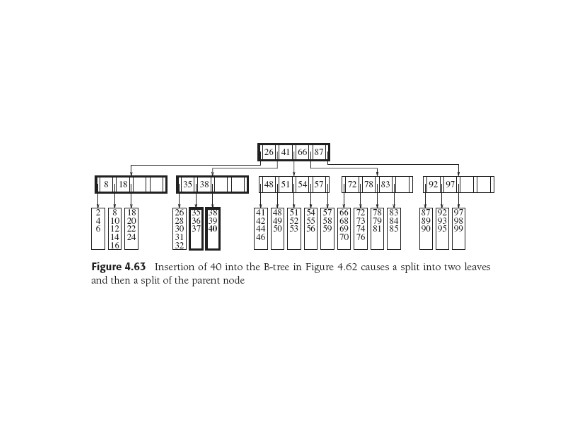
Can farm out items in overflowing leaves. To insert 29 into tree
above, could move 32 to the next leaf. Implies modification to
parent.
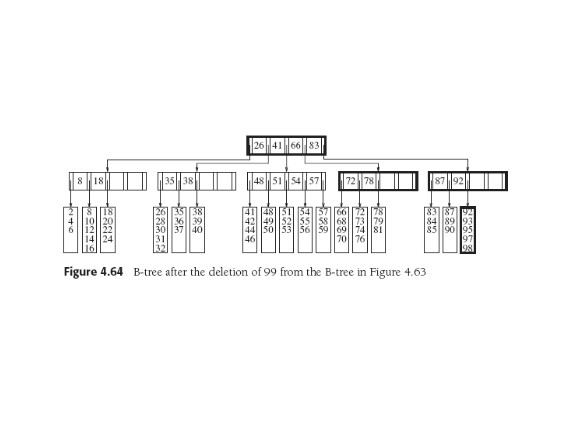
Remove 99 from this last tree: now leaf has 2 items, not enough, and
its neighbor is at the minimum of 3. So combine the two leaves into new one of
maximum length, but then the parent only has two children. So it
adapts from its neighbor with four children, and need to adjust
parents' keys.
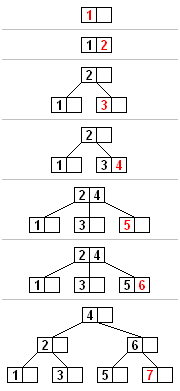
Here's a baby insert
from
Wikipedia:
Java: Sets and Maps
Weiss Ch. 4.8
These Java containers provide fast search, insertion, deletion, unlike
Java lists.
Sets don't have duplicate items, TreeSets are maintained in sorted
order with O(logN) basic operations.
Maps have (unique) keys and (possibly repeated) values. So get
usual
tests and queries (size, isempty...) and containsKey (key),
get (key), put (key, value), along with usual nonsense to allow
iterators...
Weiss of course gives a pedagogical version of treeset and treemap
implementations,
along with some cute examples of algorithms that escalate in elegance
and map use. Must reading for nascent Java power users.

Last update: 7/27/12






 (from Wikipedia)
(from Wikipedia)







