Venn Diagram
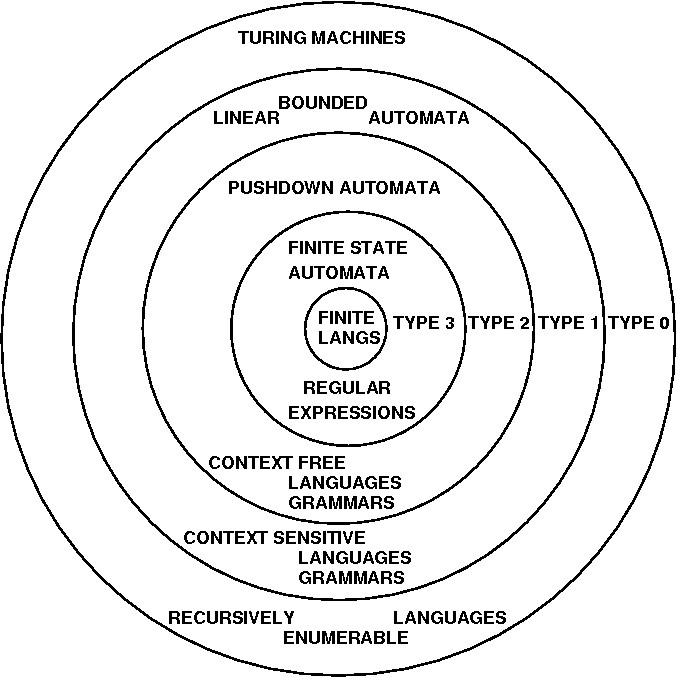

Here's a version of the infamous ``Venn Diagram''. Its rectangles
share the ``top edge'' of the page...
LANGUAGE GRAMMAR MACHINE CXTY
Finite List Enumer. O(n)
Reg. Exp S → aT RE=DFA O(n)
(ab*)*|(0*1*)* S → b =NFA=RE
Context S → aSb NPDA > Poly:
Free DPDA > O(n^3)
Lin. O(n)
DPDA
Context aS → bTSa LBA Expon.
Sensitive
Recursively Undeci-
Enumerable aT → b TM dable
Erasing Convention (EC). Limit erasing to single S → λ production, with S the start symbol. If that happens, S doesn't appear on RHS of any other productions.
Given that (have to convince self it's OK),
G is Context Sensitive (Type 1): obeys EC, and otherwise
for all
α → β, β is at least as long as
α.
G is Context Free (Type 2): obeys EC,
for all
α → β, α is a single nonterminal.
G is Regular (Type 3): obeys EC and
for all
α → β, α is a single nonterminal and
β is of form t or tW, t terminal, W non-terminal.
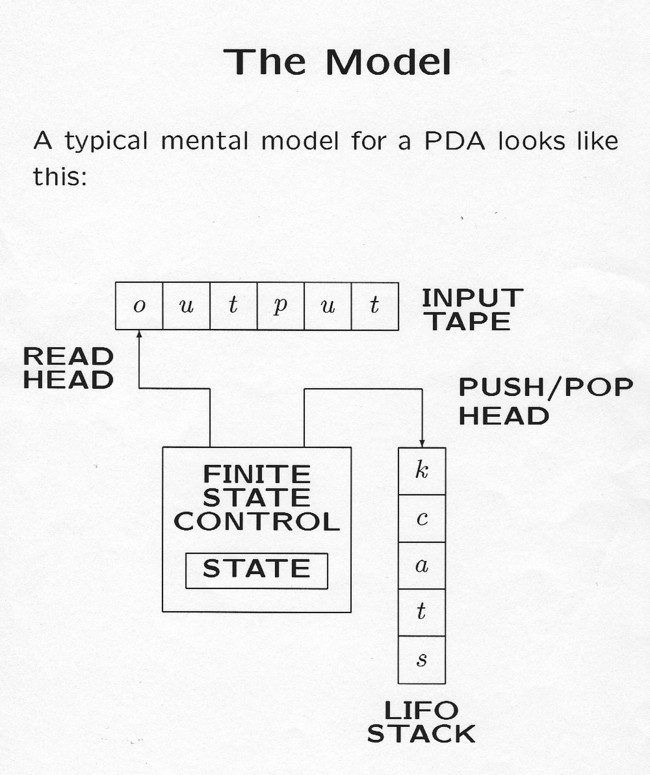


NPDAs accept context-free languages, Deterministic PDAs accept
deterministic
context-free languages. Remember palindromes, e.g.
abbabbbbabba is context free
abbabbxbbabba is deterministic context free.
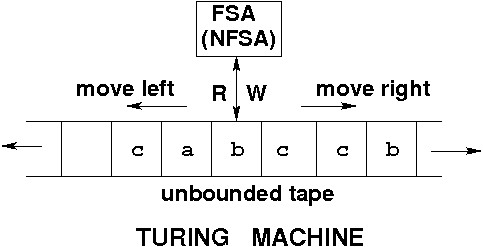
Finite alphabet, Finite number of non-blank cells, finite but unbounded memory. Cell blank or one symbol. FSA reads one cell at any given moment, then either halts or takes these actions:
Describe by set of quintuples
(current state, current symbol, symbol printed, next state,
direction).
In a deterministic TM no two quintuples have same
BUT a deterministic TM may do exponentially more work to simulate the nondet. TM (as with DFA and NDFA) -- related to the P and NP complexity class issue.
A natural question: what size (say no. of states, symbols) does a TM
need? E.g.
are 2 states and three symbols enough?
For Context Sensitive Grammars.
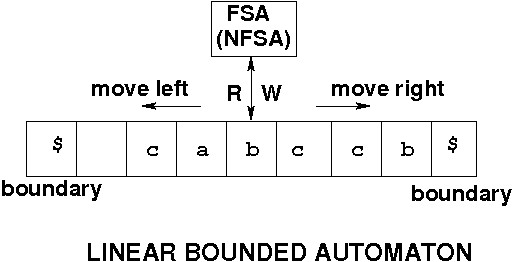
LBA is a Turing machine with the read-write head restricted to a length that is (a linear function of ) the length of the original input string.
As usual for nondeterministic machines, the NFSA version accepts if there exists a halting sequence given the input.
Context |RHS| ≥ |LHS|
|
V
a S → b R S A a
^
|
RHA longer than LHS
Context Sensitive Grammar productions
are non-shrinking only.
If you know that no derivation will ever be longer than the original input, then no intermediate sentential form exceeds that length. Thus you can bound the tape needed for the computation. Hence LBA. A TM's memory needs can shrink and grow unpredictably, hence its power.
{anbncn | n ≥ 1}
Derivation:
S aSBC aaBCBC aaBBCC aabBCC aabbCC abbcC aabbcc
Not CFG (note multiple-symbol LHSs). Also can't check the length of
three different substrings with one stack. Two you can do
(xy an bcd en zw), but not three.
LBA recognizes since non-shrinking productions mean no intermediate sentential form is longer than original input string.
Language is empty string λ and all strings with an odd
number of 0s ( > 3).
P (note shrinking productions) =
Derivation:
There are many grammars for every language. In particular, one can clearly write a CFG or Turing machine program to recognize RE languages.
Only if it needs a context-sensitive grammar, for instance, is it really a Type 1 language. Nobody seems to talk much about this, but the issue has come up in 173 exams before.