
Ordinary Differential Equations
What is a DE?
"An equation between specified derivatives of an unknown function, its
values, and known quantities and functions". For instance,
F(x,y,y') = 0
G(x,y,y',y'') = 0
a(x)y'+b(x)y + c(x) = 0
my'' + ky' +sy = g(x)
Our job is to find the function(s) y(x) so that our given equation
holds.
Sometimes solution is possible through more or less difficult analytic
techniques, sometimes we must resort to approximations, (numerical
methods, numerical solutions), with which we're most concerned here.
A Vital Issue! Using physical laws to model physical systems
as equations. Like algebra word problem. Setting up the equations is
often 9/10 of the battle and we barely touch on it here.
Derivatives and Integrals
Informally, the derivative y'(x) gives the slope of function y(x).
Likewise the integral (say from 0 to t) of y(x) measures the area
under the curve y(x).
The picture says it all:
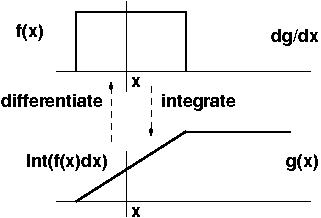
The integral is the limit of a sum; it's a continuous
sum of infinitesimals, same as a derivative is an infinitesimal
difference.
In computing, we don't have infinitesimals nor continuous numbers:
every "integral" is really a summation (unless it's a symbolic
integral, maybe in Mathematica).
DE Solutions: Integration
If we know y'(x) = g(x), then if we integrate both sides, we get an
equation y(x) = G(x), where G is the integral of g.
Hence "Solving a DE" = "Integrating a DE" and "Numerical Integration"
is approximate computer solution.
Examples:
d(axn)/dx = naxn-1, so
y' = naxn-1 means y = axn +C.
Here, C is a constant of integration. Generally DE solutions are families
of equations.
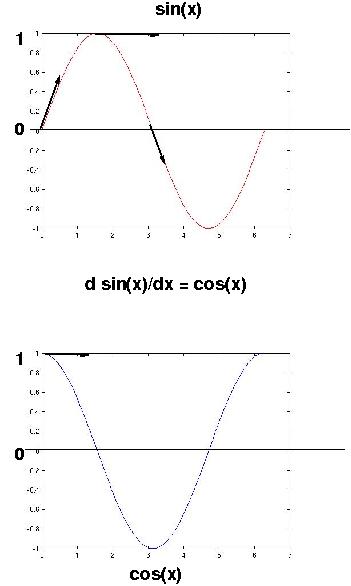
sin(x)' = cos(x), cos(x)' = -sin(x)
d eax/dx = aeax, so y' = ay means, using t
instead of x this time,
y(t) = Ceat.
Families of Solutions
As written a DE has a family of related solutions. For example,
If y'(x) = 20x3 + 14 x, then
y(x) = 5x4 + 7 x2 + C, where
C is a "constant of integration".
Can specify one of a family of solutions by specifying Boundary
Conditions (values of variables and their derivatives) it must also satisfy.
E.g. for a DE like
y'(t) = 3t2 + 13, the boundary condition
y(0) = 19 identifies a unique solution:
integrating, get y(t) = t3 +13t + C, so must have
C = 19 to get y(0) = 19.
We'll only have Initial Conditions (hence "Initial Value Problems").
Another case we won't explore
is the one where we need to
specify what happens at "both ends" of the solution for instance
("Boundary
Value Problems"). E.g. What's the distribution of temperature in a
metal plate
whose periphery is kept cooled to a constant temp (the boundary
condition) but which is being heated in the middle?
Definitions
Ordinary and Partial DEs: ordinary d/dt and partial ∂ / ∂ t
derivatives.
Order of DE: order of highest derivative appearing in it.
An nth order DE can be expressed as a system of n 1st-order DEs, as
we'll see.
Linear and Nonlinear DEs: Linear DE in y is a sum of weighted
y-derivatives of different orders set equal to 0:
a(x)y'' +b(x)y' + c(x) y + d(x) = 0
Nonlinear has more complex relations between the derivatives, like
a(x)y''y +b(x)(y'2) + c(x) √ y + d(x) = 0
Linear constant coefficient equations have solutions in exponentials
(decays, explosions, and sines)
ay'' +by' + cy + d = 0
Homogeneous and Nonhomogeneous: Hom looks like
a(x)y'' +b(x)y' + c(x) y = 0
Nonhom:
a(x)y'' +b(x)y' + c(x) y = -d(x)
Homogeneous can be a steady state solution (no 'driving force' from
outside). Any solution to a DE can have the homogeneous soln added to
it and stay a soln.
Higher Order ODEs, Systems of 1st Order ODEs
Cute trick: change a higher-order ODE (higher-order derivatives) to a
set of related first-order ODEs (first derivatives only).
Invent new variables (say u1, u2, u3,
etc.) so that the first one is y', the derivative of y; the second is the
derivative of the first, (y''); etc. So if
y''' + g(x)y'' +r(x)y' + s(x)y = t(x),
then we must have
u1(x) = y'
u2(x) = u1' = y''
u3(x)= u2' =
y''' =
t(x) -s(x)y -r(x)u1 -
g(x)u2.
There is a rather nicer (to my mind) matrix form of this, also given in the
pdf reading:
Informal DE Intro.
In Matrix Form
y''' + g(x)y'' + r(x) y' + s(x)y = t(x)
|y | | 0 1 0 ||y | |0 |
d | | | || | | |
-- |y' |=| 0 0 1 ||y' |+|0 |
dx | | | || | | |
|y''| |-s(x) -r(x) -g(x)||y''| |t(x)|
Higher Order ODEs, Systems of 1st Order ODEs
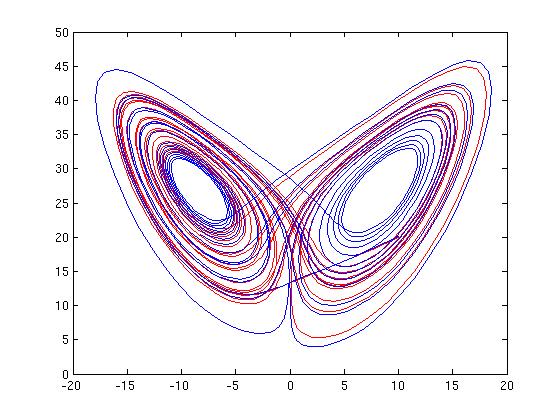
Another example of a nonlinear system of three first order DEs (The Lorenz
Attractor):
x' = 10(x-y)
y' = -xz +28x -y
z' = xy -8z/3
Which has a "chaotic" regime, solutions as below:
red and blue solns from almost identical initial conditions.
Final word. All the equations we feed Matlab to get our ODE
solving done will look like
y' = f(y,x).
Numerical Integration: The Idea
For Initial Boundary Value Problem. Assume know y(0), the given
initial condition. But y'(x) tells you how much to change y for a
small step in x. So step a bit dx along x and use y' to get a new
value
for y: in fact, just iteratively set y(x+dx) = y(x) + (dx)y'.
That's ALL THERE IS!! Everything else is just bells and
whistles.
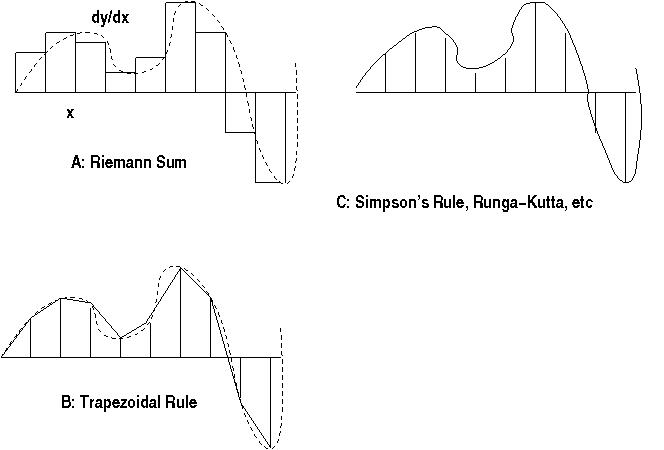
Add Rectangles, Trapezoids, or small areas from higher-order approximations:
Trapezoidal Rule, Simpson's Rule, Runga-Kutta, Predictor-Corrector...
All doing the same idea with varying degrees of accuracy, speed,
flexibility, efficiency.
Stiffness: solutions at hugely different timescales means intelligent
and varying choice of step size is needed (e.g. Matlab's ode45 and
ode45s).
ODEs in Matlab: Example I
Insult Warning! This stuff is simple!
Here's an example (PLENTY more out there in
Matlab documentation , etc.
Lorenz Attractor:
x' = 10(x-w)
w' = -xz +28x -w
z' = xw -8z/3
First Matlab needs a function that basically copies the equations above to
construct a column vector
of derivatives
y' = f(t,y)
with one row
for each of the unknowns y(i) in our equation.
In our equations there is only dependence on x,w,z, not on t.
Our derivatives
function takes two
arguments, a scalar 'time' t and a vector of unknown
variables.
So we need a little renaming of variables in the equations:
y(1) = x
y(2) = w
y(3) = z
Then we write directly from the equations (using the new
y() names) a function that looks like this:
function dy = lorenz(t, y)
% Lorenz Attractor. t a scalar,
% y a vector of y(i)'s.
% dy returned as a column vector
% of dy(i)'s
% the orig x,w,z are
% now y(1), y(2), y(3)
dy = zeros(3,1);
dy(1) = 10*(y(2) - y(1));
dy(2) = - y(1)*y(3) + 28*y(1) - y(2);
dy(3) = y(1)*y(2)-(8/3)*y(3);
end
The equations are implicitly parameterized by time, which steps along
according to a timespan parameter vector (next slide).
Running Matlab ODE Solver
Now we've got our derivatives function, which computes the
current derivative value from the
values of lower-order derivatives and the time.
We want to pass this function to another function as argument. As usual
with imperative languages, we'll pass a pointer, or a
handle for this function, given by Matlab's @ operator: E.g., either the bare
@lorenz
Or we can give it a name:
lorenzhandle = @lorenz
We need to
specify the time interval to be
covered by the integration. The documentation says it can be a 2-vector
[start, finish]
or an N-vector like
timespan = linspace(start, finish,1000)
With the 2-vector, Matlab makes up the spacing: the N-vector
provides explicit times (not necessarily evenly spaced).
We also need a (row or column) vector of initial conditions for the
system.
E.g. for Lorenz,
let's start at some point in space
(x(0), w(0), z(0)) = [10, -10,
20] .
Let's run for 20 time-units divided up into 1500 steps. We
also must be able to spell ode23, the simplest and cheapest
of Matlab's many ODE solvers.
We expect the output
to be a column vector of times (the same as our timespan input, or
made up by Matlab to lie between our start and end time), and
values of the function (and any lower-order derivatives it computes
while integrating). OK, we're off!...
%Script to Run Lorenz
lorenzhandle = @lorenz;
y0 = [10, -10, 20]; % initial conditions
%next specify 1500 instants
timespan = linspace(0, 20, 1500);
% ** boom **
[T,Y] = ode23 (lorenzhandle,timespan, y0);
% ** it's over! **
plot(Y(:,1),Y(:,3), 'r');
hold on
% new initial conditions close to previous
y0 = [10, -10, 20.1];
[T,Y] = ode23 (lorenzhandle,timespan, y0);
%BUT big difference in the two solns
plot(Y(:,1),Y(:,3), 'b');
The Plot: Y(1) versus Y(3) (X vs Z)

Matlab ODE Solver: Example II
In a vacuum, a falling body accelerates due the force of gravity.
On earth, the acceleration due to gravity is called
g = 9.8m/sec2.
Let's plot the velocity and position of a ball (in a vacuum) acted on
by
gravity. We can start the ball at what ever height and velocity we
want...
throwing it up sounds interesting (and is like the ballistics assignment).
The equation governing y as a function of time says that the
acceleration of a body due to gravity is in the "down" direction and
is always equal to g.
Assuming y measures height, that's:
y'' = -g
That's it...that's our DE to solve. Notice it's 2nd order so we'll
make a system of 2 simpler ODES.
We put that into our favorite matrix form this way.
d |y | |0 1| |y | |0 |
-- | | = | | | | + | |
dx |y'| |0 0| |y' | |-9.8|
or:
dy/dx = y'
d2 y / dx2 = y'' = -9.8
So our derivatives function in Matlab is this:
function dy = ball_der(t,y)
dy = zeros(2,1);
dy(1) = y(2); %dy/dx = y'
dy(2) = -9.8; %d2y/dx2=y''=-9.8
end
We now get to choose a start and finish time and initial
conditions. May as well start at zero time and altitude.
Let's start the ball off with an upward velocity of 100m/sec.
% script
ballhandle = @ball_der;
tspan = [0 20]; % [st fin] (secs)
y0 = [0 100]; % [ y y'] initial
[T Y] = ode23(ballhandle, tspan, y0); %boom
....
>> [T Y]
>> plot(T,Y(:,1))
>> plot(T,Y(:,2))
The Output Matrices and Plots
Notice Matlab starts out with small dt time steps, but
grows confident and starts moving along by 2 each step, which actually
leaves us with a rather un-smooth graph...
T Y VEL
0 0 100.0000
0.0000 0.0001 100.0000
0.0000 0.0005 100.0000
0.0000 0.0025 99.9998
0.0001 0.0125 99.9988
0.0006 0.0625 99.9939
0.0031 0.3124 99.9694
0.0156 1.5613 99.8469
0.0781 7.7826 99.2344
0.3906 38.3148 96.1719
1.9531 176.6205 80.8594
3.9531 318.7392 61.2594
5.9531 421.6580 41.6594
7.9531 485.3767 22.0594
9.9531 509.8955 2.4594
11.9531 495.2142 -17.1406
13.9531 441.3330 -36.7406
15.9531 348.2517 -56.3406
17.9531 215.9705 -75.9406
20.0000 40.0000 -96.0000
Velocity:
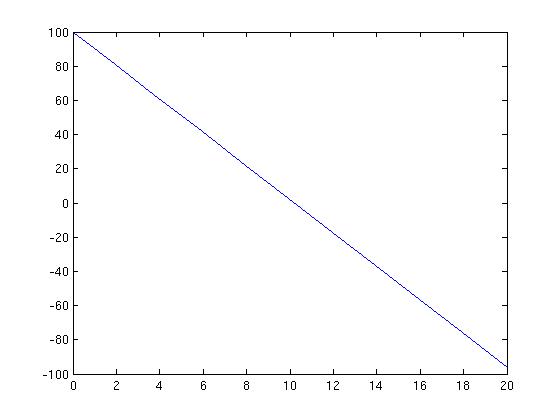
Height:

Simulations and Fun
Simulations are great fun, since we get to play around with the
rules. Suppose the force of gravity were a nice even 10, and
that its direction is reversed 10
seconds into the ball's flight?
function dy = gball_der(t,y)
if t<10
g = -10;
else
g = 10;
end
dy = zeros(2,1);
dy(1) = y(2);
dy(2) = g;
end
and
Height:

Last Words
Our goals were:
- to demystify DEs
- to encourage you as always to READ
(texts, papers, documentation, websites, tutorials) FOR YOURSELVES
- to show easy examples of solving initial-value problems with
higher-order ODEs and systems of ODEs in Matlab.
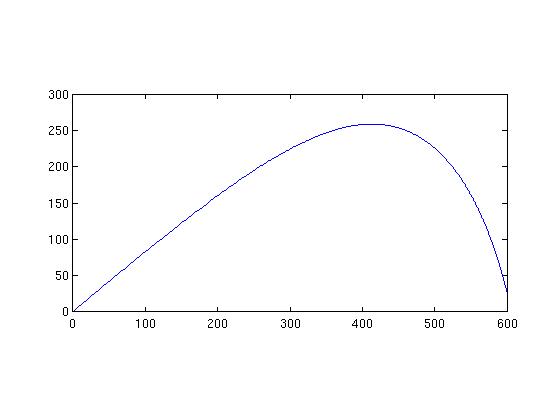
Trajectory of human head launched at 40 degrees of elevation into enemy
redoubt.
Flight took about 15 seconds. Distance unit is the meter (about 3 feet for
you Angles and Saxons).

Last update: 11/26/2013: CB










