

Look up Constraint Satisfaction Problems (CSPs) and depth-first search (DFS). Wikipedia's fine, but a very good source is the CSC242 text, Russell and Norvig's book Artificial Intelligence, a Modern Approach, Chapter 3 and the short Chapter 5. The relevant pages are on E-reserve for this class, available through Blackboard: look for reading "Russell: Constraint Satisfaction."
CSPs are a hugely important class of practical problems (e.g. classroom and job scheduling, military logistics, sudoku ...) and there are a number of more or less ingenious ways to solve them. To solve a CSP you must assign a value to each of a set of variables so that no constraints are violated. Favorite examples are cryptarithmetic puzzles like SEND + MORE = MONEY. Here the variables are the letters S, E, N, D, M, O, R, Y, possible values are the integers 0,...,9, and there are constraints like each variable represents a single integer, and the sum (in general, arithmetic operation) must work out after substituting the integer values for the variables. (See the web if cryptarithmetic is new to you. You may have worked the Prolog cryptarithmetic problem). Other examples are map coloring, where the variables are regions, the values are colors, and the constraint is that no adjacent regions can have the same color, which means respecting the specific instance-dependent constraints induced by the neighbor relations in the map.
Our last example and current exercise is to place N queens on an NxN chessboard so that no two queens are attacking one another: i.e. they are not on the same row, column, or diagonal. For more, Wikipedia -- 'Eight Queens Puzzle' -- is a place to start.
Here's an interesting line from the table Fig. 5.5, p. 143 of AIMA (again, this is in your e-reserves: see above for pointer).
Backtrack BT+MRV Forward Checking FC+MRV Min-Conflicts
N-Queens (>40,000K) 13,500K (>40,000K) 817K 4K
Here, N-Queens means the row is about the super-problem of solving ALL N-Queens problems for N from 2 to 50. The columns represent five different aproaches and the numbers are the computational cost of each. The differences are dramatic, and motivate this project. Numbers in parentheses mean 'no answer found after this much work'. More precisely, the numbers show the median number of basic consistency check operations (over five runs) for '2 to 50 queens' problems.
Let's explore the extreme (Backtracking and the Min-conflicts) solution methods.
State space search is a general Artificial Intelligence technique that gives us one way to think about CSP, and N-Queens in particular. We are searching for a legal configuration of queens-on-boards -- one that doesn't violate the non-attack constraint. The configurations are called states of the problem, and the legal ones, those that satisfy all constraints (n queens placed, no attacks), are the goal states, at least one of which we want to produce. There is an initial state from which we start our search (e.g. no queens placed), and there are one or more operators that modify states (e.g. place a queen, move a queen).
Parsing is like state-space search: the goal could be to derive the "Sentence" state and the operators are rewrite rules that operate on strings of terminals and non-terminals.
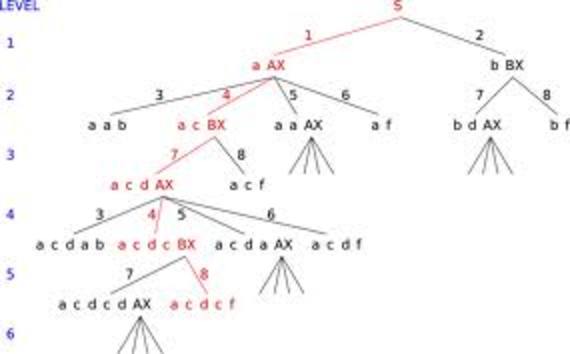
In backtracking, we build through time a search tree in which nodes contain (representations of) states, and are connected by operators. There may be several operations possible in a state. Applying the possible operators to a state yields new states, the successors of the original state: hence the tree structure. When we generate a goal state, usually we look back through the path from the initial state to the goal state to see what sequence of operators solved the problem. Luckily for us, things are a little simpler for N-Queens.
All state-space search implementations must represent the current state of the problem to allow the relevant evaluations, operator effects, etc. to be calculated efficiently.
Here, maybe the most obvious candidate is an N x N binary array with 0's for empty squares and 1's for squares with queens. This might be good for (sighted) humans, but a little thought should reveal it is too big (redundant), and not good for discovering conflicts (attacks) quickly via computer. My choice would be a Scheme vector (I like that better than a list -- why?). It is N long for the N-Queens problem and its ith element represents the ith column of the board. The value of that element is the row on which sits a queen, or -1 if the column is empty. This representation only allows 0 or 1 queens per column, which already enforces 1/4 of the non-attack constraints -- neat, eh? So a 5x5 board with three queens placed (illegally) diagonally in the first three columns would have the state vector [0 1 2 -1 -1], where -1 means 'nothing placed here'.
In this approach we start with an empty board and plunk down queens one at a time until we succeed, backing up (thus taking them off the board) when we get stuck and can't find a legal place to put the next queen.
A few things make N-queens a special case of state space search. First, if we legally place N queens we're done: that's the only goal: so that's a very simple goal test that doesn't even need to look at the state as long as our queen-placement operator doesn't cause an attack -- "count to N and declare success!" Second, the goal state is all we want to return; we don't care how we got there, so don't need to remember ancestors of search tree nodes. This is true for CSPs in general (but not true for state-space search in general: in particular it's not true for the N2-puzzle alternative assignment).
Even better, we don't need no stinkin' tree, either! It is generated by the nested calls in a recursive search (or generation) program. The whole apparatus of search-tree nodes described in Chapter 3 (and needed for the N2-puzzle) vastly simplifies: the search nodes ARE (only) the states, and the tree IS (only) the one induced in the subroutine calling stacks that are created when the search program runs.
Backtracking is simply a fancy name for depth-first search as applied to CSPs, and CSPs amount to finding legal assignments of values to variables. So you're going to write a simple, depth-limited (we only need N levels of call, right?) depth-first-search (DFS) recursive program that selects an unassigned variable (column, for us), plunks a queen legally onto some row of it (that's the value for that variable), and calls itself on the resulting one-(column or queen)-smaller problem. If that call fails, you plunk the queen in a different row in that column and try the one-smaller call again. If you can't find a legal place to plunk a queen in this column, you (i.e. your program running at this recursive level) have to fail (upwards to the one-bigger problem level). Failing thus amounts to removing the last queen placed.
True, we have computers, and search is one of AI's basic tools and fast, simple, "mindless" search is sometimes better than "thinking too much". But the interaction of complexity analysis with AI combinatorics means we can't be totally clueless. We might imagine, say, that from an initial empty-board state, a logical way to search would be to consider each column as the one for the first queen. So we'd have a branching factor of N (columns to pick) under our initial state. Under each of these column choices there's a choice of N (rows to pick in that column) to plunk the queen. So we have an N2 branching factor (level two is 'only' N*(N-1) but still...) This is a HUGE space to search. Core 2 Duos to the rescue?
Nahh, this is just too, too stupid. The combinatorics totally doom this naive approach. It takes next to no thought to see you can fix the order of the columns and not miss any possibilities: e.g. simply do col 0 at the first level, 1 next, 2 next, through N. Or pick any fixed order you like: In fact, I think working from middle columns out might be more efficient since queens in the middle of the board attack more squares (add more constraint) earlier in the search. Smaller branching factors are better, especially early on.
This fixed-order approach can itself be improved: see next section.
Fig. 5.3 on p. 142 of AIMA has pseudo-code for your backtracking CSP solver. Customized for our situation here, it looks something like this (I hope -- don't trust me though!):
function RECUR-BACKTRACK(state)
% returns solution or failure
local row, col; % local row, column index variables
if goal(state) then return(state);
endif;
col <- SELECT-UNASSIGNED-COLUMN(state);
foreach row do
if a queen on row causes no attacks, then
state[col] <- row; % update state with queen on that row, col.
result <- RECUR-BACKTRACK(state);
if result != failure then return(result); %success!
state[col] <- -1; % or whatever flag means unassigned;
% failure-- try next row
endif;
endif;
endfor;
return(failure); % can't place queen in this column in current state
endfunc;
As we noted above, one could send in a level parameter with the state, increment on success, decrement on failure (so it remembers what level we're at in the search) and when it is at N we know we've found a solution. This is the cute simplifying trick of having the goal test just checking on the level, not the state.
SELECT-UNASSIGNED-COLUMN can be a one-liner if it just implements a fixed column order, and gives another reason to send in the level: you can use the level as a column number (work left to right), or use it to index into an array the maps the level 1:1 onto a column number.
A heuristic is a rule of thumb that you believe will help in problem solving. In the context of search trees, its purpose is to help find the answer quicker, and we do that by "pruning the search" by generating or investigating fewer successors, perhaps by cutting off unpromising directions, etc. Here we invoke a simple heuristic that reduces the number of immediate successors generated at any search step, thus making a skinnier search tree with fewer states to explore at the next level. It turns out (I don't think it's obvious) that this simple heuristic does not have negative consequences (like making the search incomplete) for N-Queens.
The new idea is to SELECT-UNASSIGNED-COLUMN not in a fixed or random order, but in a principled way that varies dynamically with the search. The Minimum Remaining Values (MRV) heuristic is (for us) to choose the column with fewest remaining legal rows to plunk the queen into (minimizing branching factor). The MRV technique yields the second column (BT+MRV) in the row from "Figure 5.5" presented above.
To implement this heuristic you need to do a little more bookkeeping --- just add (carry along with, put in a list with, concatenate with... the state vector) another N-long vector to keep the number of legal rows per column, and update it for all columns when you plunk a queen anywhere. As you see from the table this turns the "2- to 50- queens" problem from 'impossible' (with a limit of 40 million operations) to possible, if still expensive.
So far our operators have been either "plunk queen" or (implicitly, on failure) "remove queen". Suppose we rethink --- suppose the initial state is a (random, best-guess,...) placement of N queens, one per column, and that the only operator is "move queen" (up or down in its column). Our job now sounds a little different: here we always have a complete solution candidate and the job is to improve it, not to create it. This strategy is a type of "hill climbing" search.
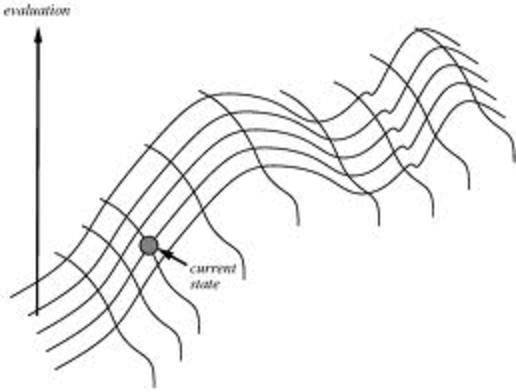
In the image, a state is a point in 2-dimensional space and the value of the state is vertical height. Here, moving along one dimension doesn't improve matters as much as moving along the other, and we also see local maxima. There's lots of work on clever hill-climbing algorithms.
This process is iterative, not recursive. Of course in Scheme you can easily keep yourself pure and unsullied by using tail recursion: this looks politically correct (and Scheme will turn it into an iterative loop behind your back.)
The Minimum Conflicts strategy works in two steps: first, pick a variable (randomly or otherwise), then assign it a value that causes the fewest conflicts with other existing assignments, and iterating.
The state bookkeeping is easy. Once again all we need is a vector recording in its ith element the queen's location (row number) in the corresponding ith column of the board.
At each iteration, to figure out what to do you first select a column somehow, then run a function that computes the location (row) where a queen in that column causes the minimum number of conflicts (you'll have to break ties somehow), and move the queen in your chosen column there.
Stealing from AIMA Figs. 5.8, 5.9, we see the program could look something like this: (state starts out as a complete candidate solution with N queens placed, and we give up after maxsteps).
function MIN-CONFLICTS-N-QUEENS(n, maxsteps) state = initialize(n); for i = 1 to maxsteps do if goal(state) then return(state); endif col <- a random column that has conflicts; row <- the row in col where a queen causes smallest number of conflicts; state[col,0] <- row; end-for return(failure)
Some design choices you can easily tweak to see if they make a
difference: this sort of variation makes for great content for writeups!
1. Either initialize the board with a random placement of queens or use a
'greedy'
process that chooses a minimum-conflict value for each variable in
turn.
2. Instead of setting col to a random column with conflicts, maybe choose the
column with the queen causing the most conflicts? You could compute
this each iteration with no change in the state representation. I've no
clue if this is a good idea!


Last update: 11/1/11