
1. Paraxial Geometrical Optics and the System Matrix
Refraction and Reflection
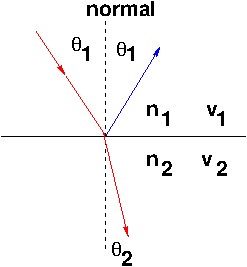
The law of refraction (Snell's Law): When a ray of light is
refracted at an interface between two uniform media, the transmitted
ray remains in the plane of incidence and the sine of the angle of
refraction is directly proportional to the sine of the angle of
incidence.
The law of reflection: When a ray of light is
reflected at an interface dividing two uniform media, the reflected
ray remains in the plane of incidence, and the angle of reflection
equals the angle of incidence. The plane of incidence is defined by
the incident ray and the surface normal vector at the point of incidence.
Snell's Law is usually written:
n1
sin θ1 =
n2
sin θ2,
with n1, n1 the refractive
indices
of the two media, where the speed of light vin a medium
of refractive index n is v = c/n if c is the
speed of light in a vacuum. Slower lightspeed in
second medium, more refraction. Here's a picture of reflection and refraction.
Using these two laws we can analyze systems of lenses and mirrors
like the all-lens system below:
After all this, we'd like to use Snell's Law in our geometrical optics approximation
to reality. Linearize problem with
paraxial rays, those that never
make
large angles with the optical axis. I.e. assume
sinθ = tan θ = θ
The paraxial Snell's Law is
n1 θ1
= n2 θ2 .
This is
a "small angle
approximation".
Suc
linear approximations describe a given function
(in some locality) as a linear function. Infinite series are
in your future!
Here,
sin(x) = x - x3/3! +
x5/5! - ...,
near 0, and for small x
we're only considering the first term.
Thin Lenses
Different rays travel
different distances through lenses, which are fatter and thinner.
So
just what happens depends on just where and at what angle the ray
enters
the lens. Inconvenient, nonlinear.
The thin lens
assumption is: "consider an infinitely thin lens" with all the
refractive
power and none of the annoying size of an actual object.
Geometrical optics uses pretty simple algebra (but pretty complicated diagrams)
to derive elegant formulae (in terms of things like radii of curvature,
indices
of refraction, and distances) that describe spherical mirrors,
refraction at spherical surfaces, thin lenses, thick lenses etc.
Focal Length
Focal length f is the
(signed) distance to the image it forms of an object at infinity.
Convex lenses have positive focal lengths, Concave negative).
The lensmaker's equation predicts the focal length of a lens
in terms of its refractive index, that of the medium it is in, and
its radii of curvature. In air (of refractive index n = 1),
one version of the thin-lens equation states that an object at
distance
s is imaged at point s' by a lens of focal length
f
if
1/s + 1/s' = 1/f.
The power P of a lens measures
how strongly it bends light, and is defined as
1/f. In an x-y plane,
We measure angles that rays deviate from the optical system
(x) axis
(rays parallel to the x-axis are at 0 radians).
Rays from the left rising in the y direction are positive.
A lens bends an incoming ray of angle θ, according to
our approximations, to give it a new angle:
θ' = θ - yP
if the ray impinges on the lens at height y.
Thus
θ' = θ -(1/f)y
The Method
-
Describe linear optical system as the product of matrices for its component
parts acting in series.
-
Describe
a ray moving left to right by its instantaneous height and
angle of flight: [y,θ]T.
-
Describe
paraxial optical elements
by 2x2 matrix transformations (ray tranfer
functions)
representing what
happens to a ray at an optical element.
- The product of the
transfer matrices describes the optical system as a system transfer
function.
Ray Diagrams
Diagram the system as thin lenses, a 2-D plot of Y versus X, with the X axis
being the optical axis.
An object being imaged is considered to be in an input plane at
the
left of the diagram (below, it's at x = 0), and the output
plane
is wherever we want to compute the final height of the
ray. Can compute (inter alia):
-
front and back focal length. The latter is just the
effective focal length of the entire system, and the former is
similarly the
focus point of angle-0 rays coming in from the right, headed left.
-
Axial image point of an object point nearer than infinity on the
optic axis. All the rays from that point are focussed there, and all
points from that input plane are the image plane contining the axial
image point.
-
Linear magnification of the system is
yf/y0, the relative height of a ray at the
input and output planes.
Ray Transfer Matrices
Consider a ray [y0, θ0 ]T
moving (translating) through a homogeneous medium. If
it moves axially by L at an angle θ0,
Its new description is
[y0 + L tan θ0,
θ0]T. The paraxial assumption is that
tan(x) = sin(x) = x, so we can describe the resulting linear
tranformation of the ray's description by
|y1| = |1 L| |y0|
|θ1| = |0 1| |θ0|
This simple matrix is how we describe the change in the ray as if
moves through some uniform medium for an axial distance.
Remember
θ' = θ -(1/f)y.
So...
|y1| = |1 0| |y0|
|θ1| = |-1/f 1| |θ0|
The
transfer matrices for spherical or refraction interfaces, spherical
mirrors, and thick lenses are similarly simple.
System Transfer Matrix
Express a paraxial system with elements described by 2x2 matrices,
say M1, M2, M3, M4 in order from left to right. Then for ray
r,
M1*r is the ray after the first element,
M2*M1*r,
M3*M2*M1*r, and
M4*M3*M2*M1 is the complete transformation and the system transfer matrix.
Note the system components appear in reverse order.
Use ray-transfer technique find:
focal points, nodal points and first and second
principal planes.
The four elements of the transfer matrix
have discernable semantics, which can be illuminated by considering
the
physical meaning of setting each one to zero. For now, though, we're done.
Example: Focal Point
Consider three lenses of focal length 200, -50, and 50 mm. The first
and second are separated by 100 mm. the second and third by 50 mm.
The
input plane is 200 mm. in front of the first lens. What is the (back,
effective) focal length of the system?
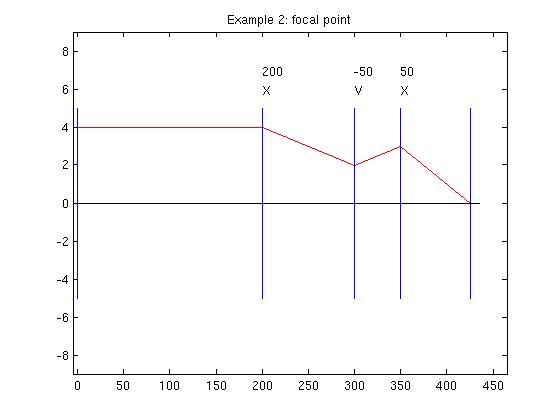
Send a ray parallel to the axis into the 6-element system
(translation, lens, translation, lens, translation, lens). The last
ray we get is the one emerging from the last lens at X=350. It turns out
to be (3, -.04)T. We're after the focal length
g= y/tan(θ), (the base of the final triangle in the
figure from X= 350 to X= 425). With the small angle assumption, the
tangent of the angle is the angle, so this ray intercepts the axis at
g= y/θ, or 75mm. We can then add a final, seventh,
transfer of this distance, which should bring the ray down to the axis
at the focal point, and that final system produced the figure above.
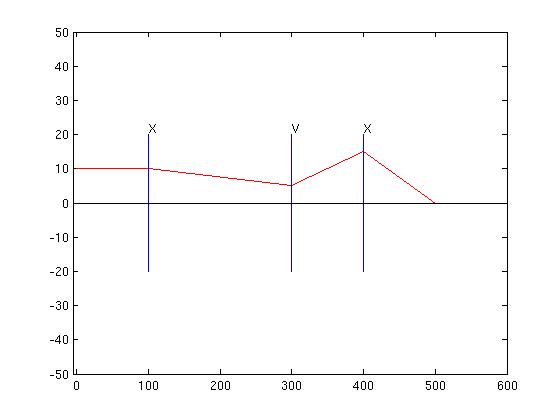
Example: Image Plane, Axial Image Point
The axial image point of a system is where the image of a ray
starting out at the origin crosses the optic axis. It's like the
focal point, and calculated the same way, only using a different
initial ray. It turns out that all the system's image points from
an object at the origin will fall in the plane at that distance, so
that is where an in-focus image will be formed.
Use slightly different 3-lens system: lenses are
spaced out by 300, 100, and 50 of focal lengths 200, -50, and
50. Shooting out a ray from the origin at angle .01 and calculating
the axial image distance (it's 95 mm. out from the third lens) we can
compose a final translation after the 3rd lens of 95 mm to get this plot:

Several Rays:
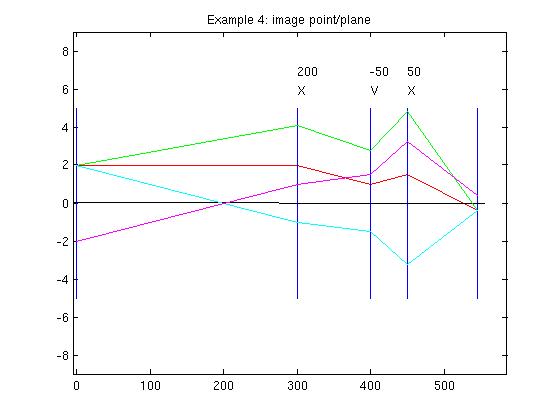
Use the y height at
the image plane to get the ratio object-height/image-height,
or
linear
magnification, as .2 (the image height is upside-down).
2. Ray-Casting and Systems of Linear Equations
The Problem and the Method
Ray-casting:
given a point
of view and direction of gaze (ray), compute the color and intensity of the
light in that direction. In geometrical optics
we follow light-paths (rays) through
optical systems with geometry, some algebra, and a few
physical laws.
Basic case: given a 3-D point of origin for the ray and its
direction, where does it intersect a given plane in space? No
different from the high-school algebra "line-intersect plane" problem, and in optics
sometimes
called "intersecting a ray with a plane mirror".
As usual, represent points p, x, r etc.in 3-D by
(x,y,z)T
vectors.
Let's represent directions α, β etc.
in 3-D by (x,y,z)T unit vectors.
They form a family that lives on a sphere of unit radius centered on the
origin. You can see that every direction corresponds to a vector (point)
whose head is on this Gaussian Sphere.
Lines and Planes
The standard way to intersect a vector with something is to stretch it out
in its direction until it hits; the resulting length is all we need.
So: Any point on a ray can be written
Ray: r = r0 + d α,
with
d the length, r0 the ray's
origin,
α
its
direction.
This vector equation represents three linear equations in x,y,z.
The plane equation is linear, and a 3-D version of the familiar line
equation:
Plane: Ax + By + Cz + D = 0
Written like this, [A, B, C]T is a vector specifying a
direction,
in fact the direction normal to the plane. Scaling the whole equation
so that this direction is a unit vector gives the new, scaled value of
D
a meaning: it's the perpendicular distance from the plane to the
origin.
Force our
infinite mirror, or plane, to pass through the origin, so we can
describe it with a linear equation: one strictly in (x,y,z)
(D = 0: no
pesky constant).
Plane through Origin: Ax + By + Cz = 0, or
(A/C)x + (B/C)y + z = 0.
For a more general raycasting project, still pretty
easy,
see
Pinholes and Beachballs (or spherical chickens!).
Intersection
The equations Ray and Plane above are four linear equations. A
solution to them gives the d at which the ray intersects the
plane,
and we're done. Preview: we write down the equations, do a quick
massage, write them in matrix form, and
the answer is obvious.
Ray origin: (x0,y0,z0).
Ray direction: (α1,α2,α3).
3 Ray Equations, 1 Plane Equation:
x = x0 + α1d
y = y0 + α2d
z = z0 + α3d
(A/C)x + (B/C)y + z = 0.
We need four equations for unknowns x,y,z,d, but clearly we
only
really need three numbers, x,y,d say, from which we can easily
solve for z using the Plane through Origin equation.
Premptively using
that equation first, we get an expression for z to substitute
into the third ray equation and we can rewrite the system as:
x0 = x - α1d
y0 = y - α2d
z0 = -(A/C)x - (B/C)y - α3d.
Matrix Formulation
Express above system as
matrix equation:
[x0,y0,z0]T
= M
[x,y,d]T ,
where M is
| 1 0 -α1 |
| 0 1 -α2 |
| -(A/C) -(B/C) α3 | .
If u = M v, then v =
M-1 u,
So we can solve (x,y,d) in terms of what
we know or can easily compute
( x0,y0,z0, M-1).
Then ignore d, put x,y into the Plane through
Origin equation, get z, and we've got our intersection-point.
References
- Tom Brown; Course Notes, Optics 211 2008, Part I.
- F.L. Pedrotti and L.S. Pedrotti; Introduction to Optics,
Prentice-Hall 1987.
- Wikipedia.
- R. W. Ditchburn; Light, Wiley Interscience, N.Y. 1963.
Last Change: 08/22/2011: CB






