
Randomized Algorithms
Weiss Ch. 10.4.
Randomized Algorithms are an important subspeciality.
They are quite important
practically, and came to prominence recently in cryptography.
The Evil Professor's Unpredictable SFS scheduling is an example from the
text. With positive reinforcement, the random schedules and amounts
of rewards makes for quicker learning and longer perseverance.
A poker player (say a computer) who has no tells and bluffs and
sandbags
randomly
forces his opponent to abandon psychology and descend to basic odds.
The
random patterns found in wildlife make for unpredictable,
rarely-reproduced behavior
that actually does not come natural to humans. Prey species naturally
make life hard for predators, but humans sometimes need security
consultants to enforce random behavior.
Enough biology.
The text considers briefly a randomized quicksort (choose a random
list element as pivot vs. always choosing the first element), which has O(N log
N) expected-time behavior and is not subject to the predictable
problems of choosing first element as pivot (e.g. almost-sorted
inputs,)
even though both approaches have worst-case
behavior of O(N2.
With randomized algorithms, there are no bad inputs (a sorted list is
always bad for the choose-first-element pivoting strategy). There
are
"bad random numbers" (a.k.a. bad luck) -- e.g. the random pivot could be smallest element of
the list every time...)
Randomized algorithms yield expected running time for any
input.
E.g. the random-pivot quicksort has expected time O(NlogN) for both a
sorted list and a random list.
We skipped over them pretty fast, but we saw randomized algorithms in
perfect and universal hashing.
We'll spend most of our time on the idea, which has applications
beyond cryptography, called
Monte Carlo (and Las Vegas) algorithms.
(Pseudo) Random Number Generators
Weiss 10.4.1
By definition, an algorithm can't produce random numbers, though
generators for crypto and other critical applications
are not only more sophisticated mathematically, but often are interactive and use
many statistics from "the world" (like disk access times, process
numbers, machine load factors,
user typing statistics, time of day, etc etc.).
Typically
applications want a stream of uniformly-distributed,
random-looking reals or ints in some range. From them other
distributions like Gaussian, Poisson, etc. can be built. Also we
may want to "replay" the random sequence to check for algorithmic
repeatability, so a user-provided seed is often an optional
feature, as are a range of more or less efficient generators.
Lots is known about pseudo-random generators, but there are still weak
ones out there in common compilers (cf. Weiss). Text- and reference-book literature goes
back to Knuth, who among other things noticed that combining a lot of
random number generators actually generated worse results. Also Knuth
analyzes the generators known at time of writing (early 1970's).
Weiss tells us about linear congruential generators, which go
back to the 1950's and which are fine for everyday use: the idea is to
compute a sequence from a seed x0 by
xi+1 = A xi mod M.
If A and M are chosen with care the sequence
repeats only after M-1 numbers.
If M is prime, they are non zero. A good pair of numbers known to Lehmer
('51) is:
M = 231 -1 = 2,147,483,647
A = 48,271.
"...with random number generators, tinkering usually means
breaking..." (Weiss p. 477).
E.g.
xi+1 = (48271 xi+1) mod (231 -1)
just (re)generates the seed 179,424,105.
Naive implementation runs into problems with overflow that affect the
random properties. Easy to fix -- if the new random number (and
state) overflows and thus
evaluates to a negative number, just add M to it (Fig. 10.55).
"Surely we just leave all this to the compiler and math library!?"
Nope, lots of libraries (thus languages) use versions of
xi+1 = (Axi +C) mod 2B,
with B the number of bits in an integer. Clearly that mod
2B should be a big red flag. In fact it makes
last bit of xi alternate beween 0 and 1 (even,
odd, even, odd...) (!!). Clearly, and likewise the
low order k bits form a cycle of length 2k
(!!).
Java and unix's
drand48 use a 48 bit linear congruential generator but return
only the high 32 bits, so eliminating short cycles but leaving long
ones that could appear in big experiments.
MAW (Fig 10-56) gives and explains a 48-bit generator using Java's
64-bit
capabilities that has better properties than the 31-bit one above.
Skip List Driveby
Weiss 10.4.2:
As in hashing, need
to know approximate number of items N to pick a maximum height logN.
Idea should be obvious, and should obviously imply (logN) insertion
and delete.
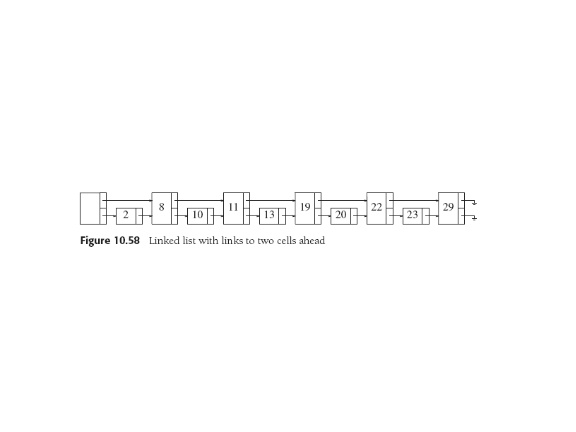
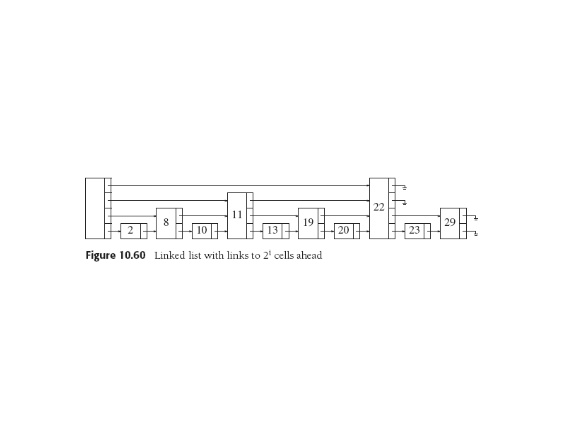
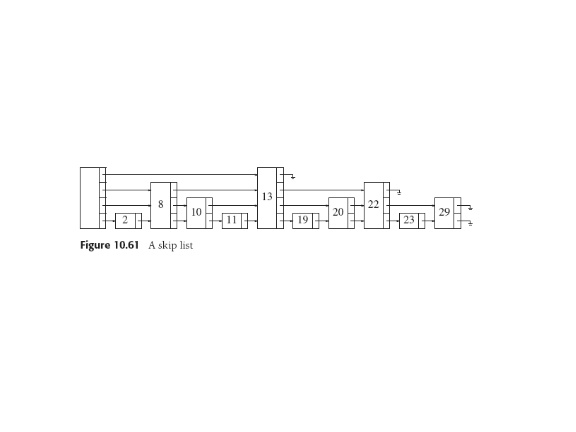
To search: start at highest link in header, follow that level until
find next node is larger than the one we're looking for or null.
Then drop to next lower level and continue. When get to level one,
node we seek is next or not there.
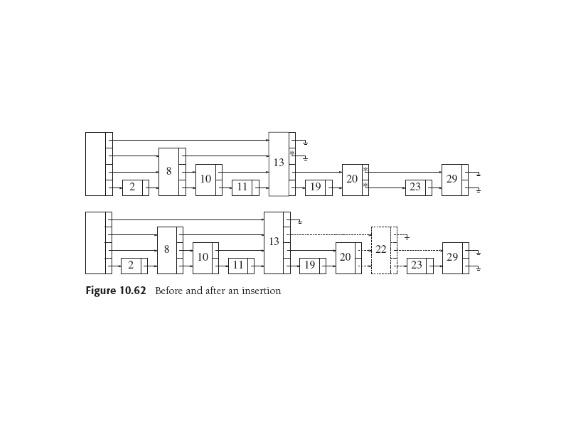
For insertion, search while marking points we drop a level. Use
repeated coin-flipping
technique to find height H such that prob(H) = 1/2H.
Thus maintain random distribution of node heights,
and the O(logN) lookup and insertion times.
(Pseudo) Primality Testing and Monte Carlo Algorithms
Weiss 10.4.3
Really it's "compositeness testing". Became critical with public key
crypto, which needs large (200 digit?) primes. Naive testing for N is to
try dividing N by every prime up to √N. Easiest implementation
is to divide by every odd number between 3 and √N, which is
about √N/2 divisions. Now if d is the number of digits in N and
we need d=200 say, then we'll need 10100 divisions: gulp.
Monte Carlo and Las Vegas algorithms (see Wikipedia, Randomized
Algorithms) are not the same as Monte Carlo simulations.
Suppose we have an algorithm to answer a question that responds
probabilistically every
time it's run. Given a composite input, half the time
(provably half the time) it says
"Definitely not" (for us, "composite!, definitely not prime"), and
half the time "Maybe so, maybe no, I dunno" (possibly prime).
Now when it says "not", it has a counter-example. The answer is
really, truly no. So if the algorithm's internal "trials" are
independent, and it answers "maybe" 20 times, then that's 20 times it
couldn't find a counter-example, which could only happen at random
one time in a million (220) if the number is composite, but
is consistent with it being prime.
So even with no definite
proof of primality, the probability the answer is "composite" is small now, and
if the answer really is "composite", that probability will only get smaller with
more tests.
Fermat's Little Theorem
A good primality test is based on FLT.
FLT is:
If P prime, 0 < A < P, then AP ≡ A (mod P).
Equivalently:
If P prime, 0 < A < P, then AP-1 ≡ 1 (mod P).
There are enough proofs of FLT to have their own Wikipedia page, which
is worth looking over. The binomial-coefficient proof is nice and the
group theory one's a 4-liner (power of abstraction). I like this
easy combinatorics one, attributed to Golumb.
Plan is to divide AP things into
two sets that account for them all. The first set will have A things
in it, and the second will have a whole number n of subsets, each of
which
is P long. Thus AP = nP +A, which implies the theorem.
AP counts the number of P-long sequences of A values,
the first sort of counting we did in combinatorics. So for example
there are 28 eight-bit bites. If A is 3, not two, we're in
trinary numbers, if A is 10 we've got decimal, etc.
We'll use binary here but notice it's without loss of generality.
With P prime, a P-long sequence has no repeated subsequences: a
6-long number can be 110110 or 101010, which look the same after a
rotation of 3 and 2 or 4, respectively, since 6 has factors 2 and 3.
With no factors, there are no repeated subsequences that take up the
whole sequence.
Let's consider A=2, P = 5 as our example.
You can't make a 5-long binary number (generally P-long A-ary number)
that's the same upon rotation. Or can
you?
Right: 11111 and 00000. So with P prime, There are A of these
special numbers in general, (2 for A=2). That leaves 30 in the
example. Let's enumerate them: plan is to pick one, generate its
rotations, which had better be all different, and of which there will
be exactly 5, then find any number not yet generated and rotate it, etc.
start rotated values
in decimal
00001 1 2 4 8 16
00011 3 6 12 24 17
00101 5 10 20 9 18
00111 7 14 28 25 19
01011 11 22 13 26 21
01111 15 30 29 27 23
Indeed. We eat up P at a time, they can't repeat within the row by
P-prime
argument above, if we pick a new one its row can never contain a
number in any other row else the whole row would be the same, and each
row has to have P entries.
Therefore we get A sequences that are just repetititions
of each value of A (eg for ternary, 000..., 111..., 222...).
Then we have the n rows each with P rotated
entries, for some integer n.
So AP = nP +A, QED.
The table of rotated values has a little structure, but it's hazy: in fact
each row shows a mini-congruential generator; some have bad
choices of seed and all have A=2, so the randomness past row 1 is actually
pretty striking.
FLT as Composite (non-Prime) Test
Simple. You give me an N to check for primality. For FLT, I must
compute
AN-1 for some A (like 2).
How do we implement the exponentiation to the (possibly huge) N?
Use the pow efficient exponentiation algorithm from
2.4.4. So the FLT test is computationally possible
O(logN)
using pow
(Weiss Fig. 2.11, p. 48).
By FLT, if AN-1 is not ≡ 1 (mod P),
we're certain N is not prime. If answer ≡ 1 (mod P) it
probably is. (e.g. 341 is the first N that fails this test for A=2).
And if we pick A = 3, 341 is shown composite). Now there are certain
numbers (Carmichael Numbers) that are not prime but satisfy our condition
for all A < N that are relatively prime to N. Smallest is 561. We
need another test! Weiss's Theorem 10.11, (related to a result we saw
in
quadratic hashing) is used in the algorithm Fig. 10.63.
The well-known Miller-Rabin primality test likewise uses another easy-to-check
number-theoretic property
and applies it at every stage of the exponentiation process. Weiss's
version seems easier to me.
Miller-Rabin a la Weiss
Back in Ch. 5.1 p. 182 we were looking at properties of quadratic
hashing and proved something about i2 (mod P) for prime table
sizes. Now this...
If P prime and 0 < X < P,
the only solutions to X2
≡ 1 (mod P) are
X= 1 or X = P-1.
Proof: If X2 ≡ 1 (mod P) then
X2 -1 ≡ 0 (mod P), so
(X-1)(X+1) ≡ 0 (mod P).
Thus, with P prime and 0 < X < P,
P must divide either (X-1) or (X+1)
and we're done.
e.g. nP = (X-1) implies X = 1.
We check this property of AN-1 at every stage of the FLT
exponentiation process in our FLT test (last overhead). If A fails
the test then N is composite, guaranteed.
But what if N is not prime? Well, the test can be fooled
(it's an "if" not an "only if").
But it's provable that for large N
at most (N-9)/4 values of A fool the algorithm. And these worst
cases are much rarer than N/4.
So if A chosen at random and the algorithm does not flunk N out,
chances are (better than) about 3/4 that N is really prime. With
probability of non-primeness
dropping by factor of four per trial, the probabiliby a non-prime will fool the
algorithm in 50 independent trials is < 2-100.
Weiss gives us the complete code in
Fig. 10.63.
One of my crypto books shows M-R working on
N= 561, the pesky Carmichal number.
If N is composite but passes FLT test AN-1 ≡ 1 (mod
N),
it is a pseudoprime for the
base A. If it also passes the Miller-Rabin test, it is a
strong pseudoprime for the base A. There are 455,052,511
primes less than 1010 with 14884 pseudoprimes and 3291
strong pseudoprimes for base (that is, A = ) 2.
In last paragraph Weiss points to work on deterministic polynomial
time primality tests. Stay tuned, the NSA is very
interested!
Last update: 12.01.14




