
ADTs
The information-hiding aspect of a Java Method
is based on the general concept of an
abstract data type (ADP).
An ADT is a set (or ordered pair):
{ {objects}, {operations}}.
Both objects and operations are specified abstractly, mathematically,
without any implementation.
Good examples are integers and floating point numbers. We know how we
want them to act in a mathematical way. Do we know or need to know
the IEEE standards for floating point representations? Do we need to
know how our particular processor does a double-precision floating
point
multiplication? Very rarely, if ever.
Should we be able to exploit
our processor's particular representation and operation, say to cut
running time by half? Not obvious...raises problems in
disseminating, maintaining, updating your code,
duplicating others' results, etc.). Information hiding is good, hence
"Methods". Why should your user know how you're representing a list?
(he shouldn't care) or be able to access your representation and
invent his own operations or modified versions of yours? (he shouldn't).
Generally, You design your ADT: what's in it, what operations it supports, what
to do about bad inputs, how to break ties, etc. Some ADTs are so well
known and useful they wind up in Data Structures texts.
List ADT
Weiss Ch. 3.1-3.5
Lists are basic data type for us all. We study their
two obvious implementations, as arrays (FORTRAN, MATLAB) and as
linked-lists (LISP).
We just said you get to make up your own ADT for lists, and that's
true. For the structures we see in 172, there are:
Constraints --- traditional
operations, cleverly-designed implementations, widely-accepted
conventions.
Freedoms --- usually a wide range of possible extensions.
Objects: An (abstract) List is a sequence
A0, A1, ...,An-1.
This list has size N. The empty list
has N=0 (useful abstraction, like null set, null string, etc.).
Ai-1 precedes Ai (i > 0),
Ai follows Ai-1 (i < N).
Predecessor of A0 and successor of
AN-1 are undefined. Aj has position
j in the list. List elements can be generic, but Weiss for simplicity
often assumes they are integers.
Operations: Our choice, but common and expected are:
print a list,
empty a
list, find item-value to return the position of first list item with
required
value, insert and remove an item to and from a given position,
find-kth to return the item at kth position. Neighbors of an
item given by
next and
previous
might be useful, as might reverse-list...etc. etc.
Array Implementation
Offhand it seems like the sequence is most obviously represented by a
simple array with items in sequence. Small matter of programming to allow
unlimited insertion without worrying about any prior maximum size
limits. W. 3.2.1 code doubles array size and copies when needed.
So, e.g., print-list is a linear operation, find-kth is constant-time.
Insertion and deletion are a mess, requiring potentially rewriting
whole array and on the average half of it, so they are O(N).
That motivates the linked list.
Weiss's Approach to Lists
Weiss brings Java iterators into all this (pp. 77-82), which for me
obscures the machine-level simplicity of pointer manipulation
(the traditional way to think about linked lists). Now
perhaps this is just my increasing out-of-touchness.
But I'm thinking for our assignments we shouldn't need much more
than simple implementations like those at
Dream in Code or
MyCSTutorials, which I recommend to your attention.
Linked Lists
It's contiguous storage that leads to O(N) insertion and deletion,
so with some overhead cost we can distribute the items and make them
basically independent. A list is implemented as a set of
list nodes, each of which has the value of a list item and a
pointer next link to its successor. Last element has null
link.
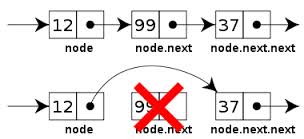
Abstractly, this is all we need. We see print-list is still linear,
but now so is find-kth since we can only visit elements by following
pointers (in LISP: "cdring down the list") N times in worst case, N/2
on average. Given we're at the right position, remove is a link
change: constant time O(1) --- Fig. above. Ditto insertion.
Doubling the number of pointers in a data structure doesn't seem like
simplification but
doubly-linked-lists remove the asymmetry of finding next and
previous nodes, and allow for more elegant algorithms with fewer
special
cases.
Such a list has pointers to the first and last nodes, and
each node has two pointers, one to previous and one to next item.
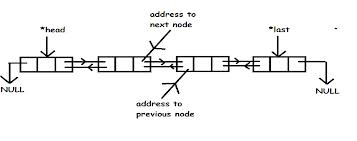
Now when writing common list processing operations these first and
last items are often annoying special cases. It's often neater also
to have a special list head node or even ADT that has pointers
to the first and last list elements. That means for instance we are
always inserting behind a node, not sometimes in front,
say to add a new first element. Similarly, a sentinel or tail
node can be put at the back of the list, so that operations on the
last node are the same as on a middle node.
Java Collection API
This is Java, not data structures. ;-}.
Get to know and understand the collection routines, which are probably
numerous and have obvious names. (W. 3.3.1). Important concept, if
it's new to you, is the iterator; in fact collections extend the
"iterable" interface, which allows elegant enhanced for loops that
look like
for( my_item : a_collection),
which serially assigns items
from collection to my_item and executes the loop.
There are (dis)advantages to using the iterator interface:
ad: shorter, elegant-looking code
disad: you have to understand more or less arcane properties of Java's
implementation, which defeats the purpose of the
ADT idea or at least damages its elegance.
Never mind. More clearly related is the
Java List interface , which
extends the Java collection. Operations get, set,
add, remove, size...
It supports
array and linked list types. You know the advantages and dis- of
these by now. Arraylist automagically adjusts its size as necessary.
Weiss has some little implementations of easy list jobs, with a simple
but vital analysis of their running times.
Quite good stuff,
pp. 64-65. Check out the alluring but disastrous quadratic (!) routine using
Arraylist
to add up the list elements....a lesson for us all.
W. 3.3.4 is an example of removing all even-valued items from a list.
He walks us thru the considerations, plus examples of code that looks like it should
work but doesn't -- examples of the disad above.
Included is the idea he points out
earlier that with an iterator, you know your position if you want to
remove an element, so it goes lots faster since you don't have to
navigate to that position. Also he has some run-time numbers showing
the informed (linear) method runs in .07 seconds for a 1.6M long list and the
naive (quadratic) method takes 20 minutes.
W. 3.3.5 points out there's a Listiterator that specializes iterator
to be more useful for lists. Enjoy.
Arraylist and LinkedList Implementations
You actually know enough to write your own list library
for array or linked implementations using the simple approach alluded
to above in the outside links. AND you've got lots of free power
that Java hands you on a platter.
Weiss provides
a pair of free-standing re-implementations of
arraylist and linked list libraries using built-in Java classes like
collections and iterators. If this is your style, great: it takes
full advantage of Java's power.
It is eemingly thorough and seems at least modestly
helpfully-described. Reimplementation of language features
in the language itself is
a very common tutorial device (esp. in LISP and Prolog)
and shows "how things work" under the hood, perhaps.
You're encouraged to write code you understand yourself: it's quicker
than trying to debug something you don't. Using existing code is OK
with me, just remember to give credit where it's due by referencing where you
copied from. Tact! Professionalism!

Last inspection: 5/27/14



