Family of Formalisms
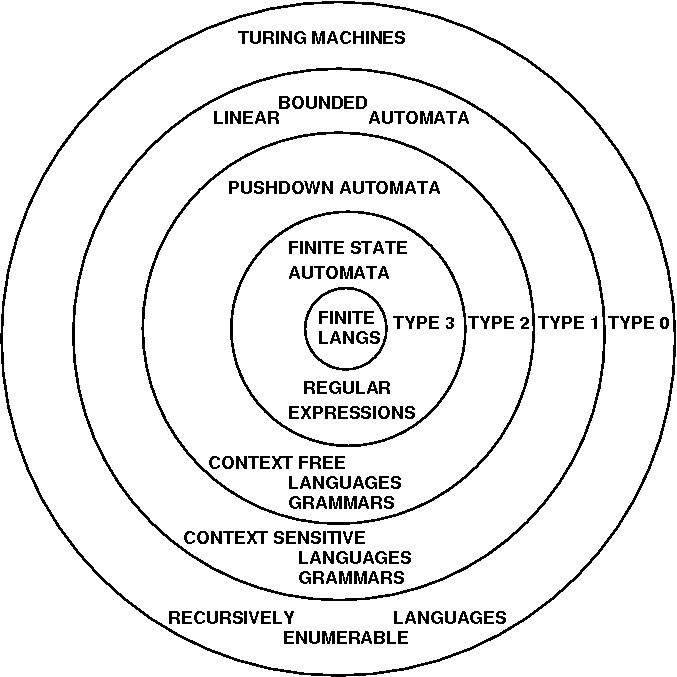

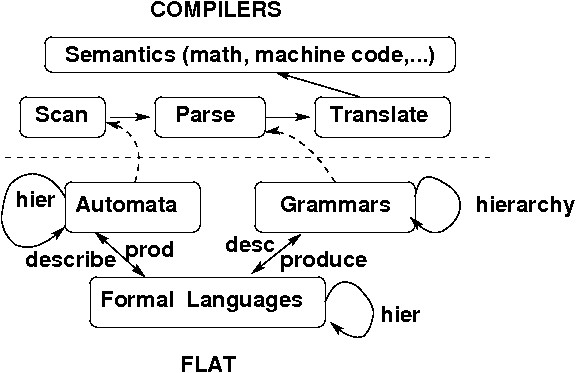
Very important practically (scanners). Good introduction to idea of describing languages through grammar-like and machine-like formalisms, and through programs.

A few trifling issues: Childhood development, learning, word segmentation, word recognition (scanning?), parsing, NL grammars, intention, ambiguity, intonation, planning,physics, common sense reasoning, temporal and physical context, dialogs and story, corrections and questions, use of vision, pronoun reference, philosophy of language, speech acts, other minds, neuro-anatomy, statistics, evolution, anthropology...
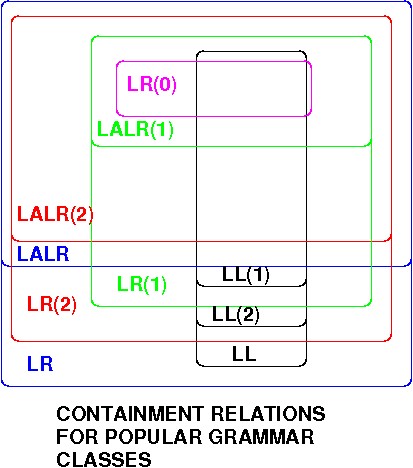
This includes practical (parsable in reasonable time) classes for computer languages. (See Michael Scott's reading on Blackboard, buy his text.).
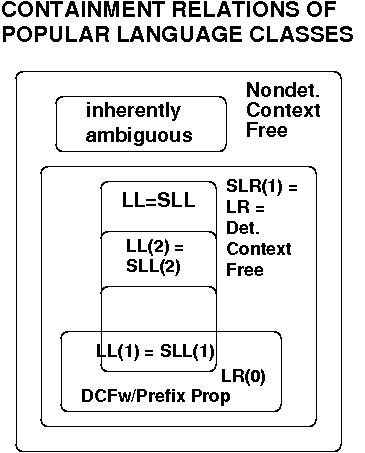
Likewise, some grammars have nicer, or different properties from closely-related ones, or even others for the same language: choice of language and grammar is important in designing and implementing a computer language.
Finite Automaton is quintuple:
Notation varies, but here
S is a set of N states, S0 is a special starting state and
F a set of final (``accepting'') states. C is the set input symbols
(the alphabet), T is a function (for a deterministic
automaton)
Start in start state, if next input symbol matches label on transition from current state to new state, go to new state, repeat. If not at EOF and no moves possible, reject. If EOF then accept iffi in accepting state. (don't want to have to be at EOF? then convert your FA to one with loops on F states that gobble rest of input). Similarly can fix FA so it never gets ``stuck''. Choice: FA produces output or performs other actions either at each state (Moore machine) or, as in 173, on the transition (Mealy machine).
Recognize words with at least 3 x's (4 states). A is set of
characters in alphabet.

Recognize Pascal variable names (letter followed by one or
more letters or digits) (2 states). N is set of digits.
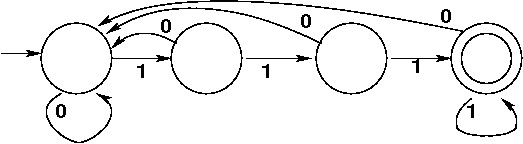
Recognize binary strings ending in 111 (4 states).
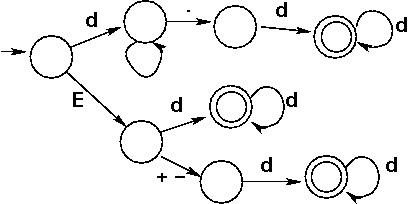
Recognize real numbers in Pascal (one or more digs followed by (a) a
dot followed by one or more digs, or (b) an E followed by either one or
more digits or a plus or minus followed by one or more digs.) (8
states).
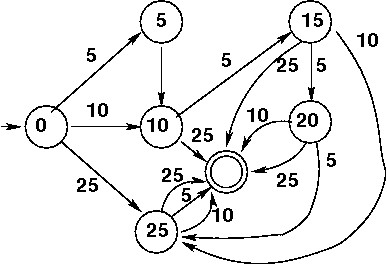
The cigarette machine here in the hospital
accepts nickels, dimes, quarters, needs 30 cents or more
(7 states). Sorry, it doesn't make change! (need loop on accepting state?)
Lots of choices: often switch (case) statements.
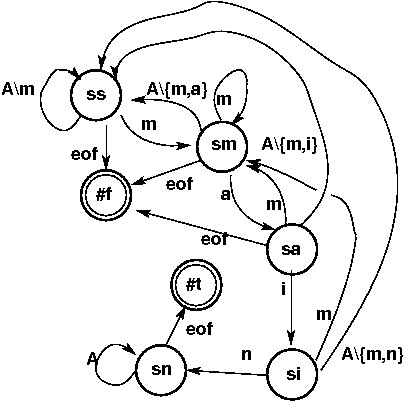
Pseudo-code for finding 'main'.
1 repeat // look for an 'm'
read c; if eof, fail
while c != 'm'
2 repeat // got 'm'; now 'a'
read c; if eof, fail
while c == 'm'
if c != 'a' return to step 1
3 read c; if eof, fail // got "ma"; now 'i'
if c == 'm' return to step 2
if c != 'i' return to step 1
4 read c; if eof, fail // "mai";now 'n'
if c == 'm' return to step 2
if c != 'n' return to step 1
5 got it; skip rest of file and succeed
Think of as graph: each node a step, each arc a transition between steps, labels on arcs give inputs causing transititions.
enum {ss, sm, sa, si, sn} state = ss;
char c;
bool accept = false;
while (c = getchar()) != EOF
switch (state)
case ss:
if c == 'm'
state = sm;
case sm:
switch (c)
case 'm': ; // stay in sm
case 'a': state = sa;
default : state = ss;
case sa:
switch (c)
case 'm': state = sm;
case 'i': state = si;
default : state = ss;
case si:
switch (c)
case 'm': state = sm;
case 'n': state = sn;
default : state = ss;
case sn:
accept = true;
print (accept ? "yes" : "no");
This code consumes all its input but note that scanners don't: they find longest acceptable prefix and send that to the application, expecting to be called again for next token. Note Fortran's DO 100 I=1,50 or DO100I=1.50 problem or Pascal's 3.14 vs 3..14 problem.
RE is algebraic formula, a pattern, describing a set of strings called the language of the expression.
Operands:
* symbol from the RE's alphabet.
* variable, whose value is pattern defined by RE
* ε or λ, the empty string
* NULL or φ, the empty set of strings
Operators:
* Union or alternation (∪ or | ):
* Concatenation:
* Kleene Closure: R1 repeated 0 or more times:
Precedence: closure, concat, union.
Over {0,1}:
* End in 3 consecutive 1's:
* Have at least one 1.
* Have at most one 1.
Over {A..Z,a..z}:
Let
Contain the word "main".
Contain 3 x's.
Pascal identifiers.
Let
Have a fractional part, an exponent, or both (else it's integer).
if fractional part, must be at least one digit on
each side of decimal point.
In an exponent: sign is optional, must be at least one digit.
Let [digit] = 0|1|2|3|4|5|6|7|8|9
Let [unsigned_int] = [digit] [digit]*
Let [exponent] = 'E' | 'e'
Let [sign] = '+' | '-' | ε
Let [fraction] = ('.' [unsigned_int] ) | ε
Let [unsigned_real] =
[unsigned_int] [fraction]
( [exponent] [sign] [unsigned_int] | ε)
Remember: abbreviations like [digit] do not change the power of the notation. Proof: expand them all out in-line (they aren't allowed to be recursive).
N.B. They are universally written with angle-brackets:
RE's ubiquitous in UNIX (also Perl, scanf etc.):
In shell command lines
Within text editors
pattern matching programs such as grep and egrep.
C's scanf has hidden powers: e.g.
scanf("%[ ∧ \n ] \n", &line);
Here the ∧ means "not" (sorry!).
For conciseness and convenience, Unix recognizes additional operators, of course definable in terms of the primitive ops: e.g:
character classes: '[' [list of chars] ']'
start of a line: '∧ '
end of a line: '$ '
wildcard: match any char but newline: '.'
optional instance: R? = ε | R
one or more instances: R+ = RR*
These extensions vary considerably between languages, tools. E.g. it is common to have a match bind what's matched to a variable, so that variable can be used in future matching patterns.