Lambda Calculus 4
TYPES
Implement typing and familiar data structures in λ calculus.
All we have is functions and names, but no restrictions on
operations between them: e.g.
iszero true ==>
λ n (n select-first) true ==>
true select-first ==
λ first. λ second. first select-first ==>
λ second. select-first ==
λ second. λ first. λ second. first}
a function of 3 args that returns 2nd... but it seems
pretty meaning- and useless.
Bad old days: Machine code and BCPL. Need types for familiar reasons.
Ultimately, get Java that is very rule-bound about types.
IMPLEMENTING TYPES
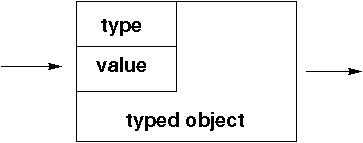
Typed objects have a type and a value.
Construct them, extract value or type, test the type, and
handle type errors.
One idea: use integers to represent
types and to use numerical comparison for type-checking.
λ calculus implementation: pair functions (of course):
Typed objects represented as type-value pairs.
def make-obj type value = λ s. (s type value)
def type obj = obj select-first
def value obj = obj select-second
STRATEGY
Define (dynamically) typed objs, ops, in terms of untyped:
- Check argument types.
- Extract untyped values from typed args
- Carry out untyped ops on untyped vals
- Construct typed result from untyped result.
Start with untyped operations, which is what we have (and like machine
code), but only use typed ops on typed args to avoid overriding
checks.
Use UPPER CASE LETTERS for typed constructs, lower for untyped.
ERRORS ETC.
Type errors can be represented by integers, say:
def error-type = zero
def MAKE-ERROR = make-obj error-type
which expands as
make-obj error-type ==
λ type. λ value. λ s. (s type value )
error-type =>
λ value. λ s. (s error-type value).
Then can define ERROR, iserror, etc..
Go on to implement
and check for
type errors, and how to implement typed booleans, conditionals, numbers and
arithmetic, and characters. Static and dynamic type-checking.
TYPE Examples:
Booleans, types
def bool-type = one
def MAKE-BOOL = make-obj bool-type ==
λ value. λ s. (s bool-type value)
def TRUE = MAKE-BOOL true ==
λ s. (s bool-type true)
def FALSE = MAKE-BOOL false ==
λ s. (s bool-type false)
def isbool = istype bool-type ==
λ obj. (equal(type obj) bool-type)...
Boolean Function Example
def NOT X =
if isbool X
then MAKE-BOOL (not(value X))
else BOOL-ERROR
More TYPE Examples: Numbers and Arithmetic
Normal approach: with MAKE-NUMB, error object, isnumb, etc. then:
def SUCC N =
if isnumb N
then MAKE-NUMB(succ(value N))
else NUMB-ERROR
Numbers...
def 1 = SUCC 0
def 2 = SUCC 1
...
So 1 expands to an isnumb test
(7 or so lines to derive true) and a MAKE-NUMB,
which takes 8 lines to turn into
λ s. (s numb-type one).
NEW NOTATION
Allow Infix: add rewrite rules like
< exp1 > AND < exp2 > == AND < exp1 > < exp2 >,
similarly for OR, +, -, *, /. No precedence or associativity.
Type structures: Lists of definitions: e.g. Booleans are
defined as lists of definitions, and Boolean
functions are too:
NOT TRUE = FALSE
NOT FALSE = TRUE
But to implement the definition we use conditionals:
def NOT X =
IF X
THEN FALSE
ELSE TRUE
Henceforth, we can define Boolean functions by using TRUE and FALSE
in place of X
with this sort of notation:
def NOT TRUE = FALSE
or NOT FALSE = TRUE
...another e.g.
def IMPLIES TRUE Y = Y
or IMPLIES FALSE Y = TRUE
STRUCTURE MATCHING
When a fn with multi-case def. applied to arg, the arg is matched
against the structured bound variable (or constant or constructor
sequences) to see which case applies: use the bound variables from
that case. Structure Matching!.
In our functional notation, we have to use conditional expressions explicitly to determine
the structure and figure out the case, then use explicit selection of
substructures from structured arguments.
Recall that PROLOG does structure-matching directly (through
unification), and
uses structured arguments like
FOO([X | L], [H | T]).
We'll extend our emerging λ-calculus-based
language to include structure matching (purely through syntactic
sugaring).
We've seen the syntax for cases (our e.g.: Booleans) --
IF-THEN-ELSE, def or.
Example: NUMBERS and STRUCTURE MATCHING
With numbers, we allow zero and bound variables qualified by nested
SUCCs in place of b.v.s: e.g. sum of first X ints:
SUM 0 = 0
SUM (SUCC X) = (SUCC X) + SUM(X)
Which we had to write
rec SUM X =
IF ISZERO X
THEN 0
ELSE X + (SUM(PRED(X))
We can now write
rec SUM 0 = 0
or SUM (SUCC X) = (SUCC X) + SUM(X)
...similarly
rec POWER X 0 = 1
or POWER X (SUCC Y) = X*(POWER X Y)
LISTS, STRINGS
The list data structure holds a variable length sequence of values.
We can develop list constructors and accessors using pair
functions (AGAIN!!).
Obviously, the pair represents the HEAD and TAIL (CAR,
CDR) of the list. It is fairly straightforward to
introduce simpler list notation and
produce needed list utilities, including list comparison, indexed
access (a,k.a arrays),
and mapping
functions (like mapcar in Scheme or LISP.)
Strings can be represented
as lists of characters, and we can even work out numeric
string to number conversion.
LIST Example defs
def CONS H T ==
if islist T
then MAKE-LIST λ s . (s H T)
else LIST-ERROR
...and our fave
rec APPEND L1 L2 =
IF (ISNIL L1)
THEN L2
ELSE CONS (HEAD L1) (APPEND (TAIL L1) L2)
A new Prolog-like notation for lists is easy to define:
:: for CONS, [ ] to delimit lists,
NIL == [], etc.
LIST STRUCTURE MATCHING
Flatten [[1,2],3] goes to [1,2,3]. Empty list is flat, if head is not
a list join it to flattened tail, else append flattened head to
flattened tail.
rec FLAT [] = []
or FLAT(H::T) =
IF NOT (ISLIST H)
THEN H::(FLAT T)
ELSE APPEND (FLAT H) (FLAT T)
Note, in LISP, no case definitions OR structure matching: explicit
list selection is necessary.
Generally, objects are defined by a constant base cases and structured
recursion cases, so their definitions have base cases with constants
for matching constant arguments, and recursion cases with structured
bound variables for matching structured arguments (above, []
and
[H::T]).
COMPOSITE VALUES AND TREES
Use lists for ``structs'' (as in Prolog, Scheme, LISP...). Need
accessors and updaters.
Generalize structure matching by using selector functions and
allowing arbitrary bound variable lists that include explicit or
implicit empty lists.
Important operations (e.g. sorting, searching) inefficient with
lists: introduce trees.
We won't do any details here: they are quite straightforward and
methodical and the result is we can implement all our CSC172 algorithms
on linked lists and trees.
EXAMPLE:
E.g. of generalized structure matching and
a new list notation: Here's
three-field record for stock control:
< < item-name > , < stock-level >,
< reorder-level > >
Define selector functions:
def ITEM [I,S,R] = I
def STOCK [I,S,R] = S
def REORDER [I,S,R] = R
The bound variable list is a list, i.e. ends with NIL, so
[I,S,R] == I::S::R::NIL.
This matches the argument and we get assignment of I
as item-name function, etc.
LIST OF RECORDS
Bound variable [I,S,R]::T matches a list with T
matching the TAIL of the list (Prolog-like).
A function to find all items whose level is
below the reorder level recursively builds and returns
a list of such records.
rec REORD [] 0
or REORD ([I,S,R]:T) =
IF LESS S R
THEN [I,S,R]::(REORD T)
ELSE REORD T
LOCAL VARIABLES
DESIRE:
notation for local variables, which are of course name-value
associations for use within an expression.
HOW? What do you think?
HINT: There's only two things it can be: abstraction or
application.
Consider:
λ < name >. < body > < argument >
Requires replacement of all free occurrences of
< name >
in < body > with < argument > before evaluating
< body >.
Just what we want from a local variable, no? We use
let < name > = < argument > in < body >
to express the "local variable" semantics of this application
(variable binding).
P.S. We've seen Scheme uses exactly this implementation for let!
CURRIED FUNCTIONS
May see this in readings. Haskell Curry noticed you can
implement a nest of single-argument function calls with one
multi-argument function call and vice-versa.
E.g. ((f(x)y)z) is the curried form of the uncurried
f[x,y,z].
Converting
curried function
to uncurried
function and back is easy. The curried one is the nested one with single
arguments.
Thus by using the currying function we can now write
def SUM-SQ1 [X,Y] = (X*X) + (Y*Y)
(We've come a long way!
looks like a
(weakly) typed programming
language, (but we know it's all just functions!)
CURRYING
Recall: def curry f x y = f [x,y]
Now if: def curry-SUM-SQ = curry SUM-SQ1
RHS expands to
λ f. λ x. λ y. (f [x,y]) SUM-SQ1 =>
λ x. λ y. (SUM-SQ1 [x,y])
so
def curry-SUM-SQ x y = SUM-SQ1 [x,y]
thus the nested, curried form is the same as the argument-list form.
Likewise
def uncurry g [a,b] = g a b
works in reverse.
PARTIAL APPLICATION
Common in λ
calculus since we've used it from the start!
Generally, idea is to create a new function from a multi-argument function by
supplying some of its arguments.
Happens
automagically with nested single-argument functions.
Lots of ILs don't allow
functions as objects: can't get new functions by
partial application: instead, obvious ploy:
New fn calls old one with parameters frozen in:
function add-1 (x)
return add(1,x);
FINALLY
we have now developed a rather high-level, weakly-typed
functional language that actually begins to look like, say, Scheme.
Recall we can always get back to pure λ
calculus by simple, unambiguous substitution rules.
The
appearance of a big ontology
of functions, values, structures... but they're really all
pure λ functions interpreted in different ways.
All these things are ``really'' the same and
therefore we can't type-check them -- so we can't for instance
constrain selector and constructor functions for data structures to
have appropriate arguments.
Our weak type-checking will detect some
clashes when functions are evaluated, but in principle we can still
apply anything to anything else, which definitely will produce a fine
λ expression --- but it may not have any plausible
interpretation.
FINAL WARNING!

(< name > < argument >) ==
( < function > < argument >)
We'll soon have names for functions like identity
and concepts like true two,...
For your sanity and success remember NEVER to expand a name
until it is the function you want to apply, as above!
This saves you from useless and dangerous copying of complex
substructure that is best notated by its simple name.
E.g.
(self-apply ((apply identity) apply)) ==
(λs. (s s) ((apply identity) apply))
Not
(self-apply ((apply identity) apply)) ==
(self-apply ((λ func. λ arg. (func arg)
identity) apply)
BUT...! With applicative order, we'll have the luxury of
evaluating arguments before functions. Then it's a judgement call,
but often useful to do that. Here, clearly, (with -> as a new
notation
for applicative order reduction):
(self-apply ((apply identity) apply)) ->
(self-apply apply)

