Achieving the metric calibration
Let the Euclidean camera projection matrices be
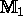 and
and 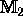 .
.
Since 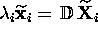 , by comparing
, by comparing
- Euclidean equations:
-

- Projective equations:
-
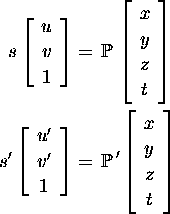
we have

3D reconstruction after going back to Euclidean space
The Euclidean projection matrices are available HERE for the first image and THERE for the second image. The
Euclidean structure of the bi-plane object is
available HERE for the first
image.
Back projection of the Euclidean reconstruction onto the first image

Orthographic projection of the Euclidean reconstruction on to a plane orthogonal to both planes of the calibration apparatus

The result is not perfect, but this is because the image of the
calibration apparatus is very small, and that the corner points
cannot be precisely localized. We are happy with this
result :-) remembering that the classical calibration technique
does not provide any useful results. A more reasonable example is
shown here.
Author: Zhengyou Zhang
Email: zzhang@sophia.inria.fr
Thu Oct 10 15:49:19 MET DST 1996
![]() and
and ![]() .
.
![]() , by comparing
, by comparing

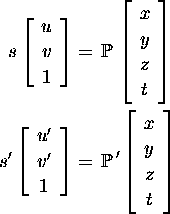
![]()

