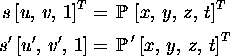
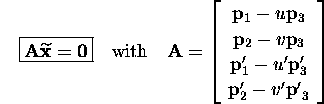
with ![]() , the i-th row vector of
, the i-th row vector of ![]() .
Since the projective coordinates are defined up to a scale factor, we
can impose the constraint:
.
Since the projective coordinates are defined up to a scale factor, we
can impose the constraint: ![]() .
The solution is simply the eigenvector of
.
The solution is simply the eigenvector of
![]() associated to the smallest eigenvalue.
associated to the smallest eigenvalue.
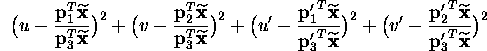
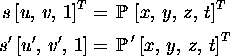
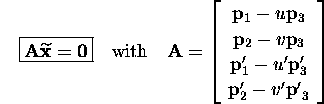
with ![]() , the i-th row vector of
, the i-th row vector of ![]() .
Since the projective coordinates are defined up to a scale factor, we
can impose the constraint:
.
Since the projective coordinates are defined up to a scale factor, we
can impose the constraint: ![]() .
The solution is simply the eigenvector of
.
The solution is simply the eigenvector of
![]() associated to the smallest eigenvalue.
associated to the smallest eigenvalue.
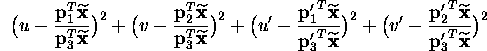


Author: Zhengyou Zhang
Email: zzhang@sophia.inria.fr